This page is a sub-page of our page on Disagreement Management.
Related KMR pages:
• Knowledge Negotiations
• Modeling and Mapping
• Asynchronous Public Service
• Common Sense
///////
Other relevant sources of information:
• This Life: Secular Faith and Spiritual Freedom – a conversation with Martin Hägglund from the pod Life after God, on YouTube
• This Life: Secular Faith and Spiritual Freedom, by Martin Hägglund.
• Martin Hägglund – This Life: Why Mortality Makes Us Free, lecture by Martin Hägglund at the University of York Audio Visual Centre, 30 Oct 2019.
• This Life: Why Mortality Makes Us Free, by Martin Hägglund, 2019.
///////
1. INTRA- AND INTER-CULTURAL CONCEPTUAL DISCOURSE
1.1. What is a Concept?
A concept is a representation of something that we have experienced or that we can imagine and which we can apply to the objects that we are conscious of.
Here is a list of properties for the concept “concept”:
• A concept must always be defined by making use of other concepts.
• A concept can be designated by one or several different names (= symbols).
• A concept is always idealized, i.e., it contains simplifications that emphasize some aspects and omit others.
• The definition of a concept always depends on the context within which, the purpose for which, and the target group towards which the concept will be used.
• The aim in concept construction is always to disregard the inessential aspects
and focus on the essential aspects for the given context, purpose, and target group
of the concept under construction.
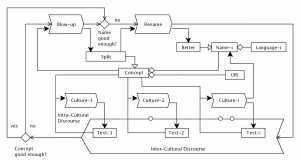
1.2. A Bottom-Up Driven Intra- And Inter-Cultural Concept Improvement Process
Based On Disagreement Management
Figure 1 presents a model of such a bottom-up driven conceptualization and vocabularization process. In this model, a \, C_{oncept} \, initially has a URI and a \, N^{ \,i}_{ame} \, in the \, L^i_{anguage} \, spoken by the \, C^{ \,i}_{ulture} , which could refer to a large or a small sub-domain of the overall human culture.
Within each \, C^{ \,i}_{ulture} \, there is an intra-cultural discourse on the relevant properties and examples of the \, C_{oncept} \, , and the results – i.e. the intensive and extensive descriptions of the concept – are documented in the outcomes \, T^{ \,i}_{ext} \, .
Moreover, the different cultures take part in an inter-cultural discourse, a knowledge negotiation process which aims at calibrating the different names and textual descriptions in two different ways:
(i) by renaming or redefining concepts that are not well-enough named or defined, and
(ii) by splitting (= blowing up) concepts that are not coherent enough – in the sense of lacking enough alignment between their intentive and extensive descriptions (See below).
1.3. Calibrating concepts by aligning intentive and extensive definitions
This alignment between the intentive and the extensive descriptions – i.e., between the properties and the examples – of a concept can be monitored using the framework of
Formal Concept Analysis, as described below in Section 1.9 below.
Rules: The definition of a concept captures the concept’s intention. It represents the properties that the concept aims to express and delimit with respect to its surroundings. To define a concept by describing its characteristic properties is to describe it intentively.
Models: The examples of a concept capture the concept’s extension. They form the set of objects that belong to the concept. To describe a concept by pointing to its characteristic examples is to describe it extensively.
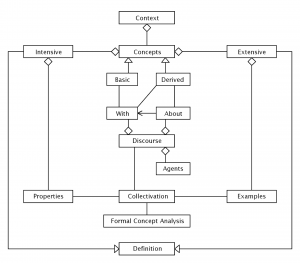
1.4. Basic concepts versus derived concepts
Moreover, as modeled in Figure 2, within each context (= community = discourse = … ) D some concepts are basic (= primitive). The basic concepts of D are not explained (= talked ABOUT) within D but only used (= talked WITH) in order to explain (= express) other concepts.
These other concepts are called derived concepts. Once a concept has been derived (= talked ‘about’ = explained) within D, it can be used to talk ‘with’, i.e. to help explain other concepts within D.
////////// Build-up for the theory-practice example
1.5. Basic concepts
Basic Concepts for a discourse can only be talked WITH (= in terms of) and never talked ABOUT (= defined) within this discourse. Whenever something is talked WITH, we have to check that it is either a basic concept, or that it has already been talked ABOUT.
1.6. Derived concepts
A concept is talked ABOUT when it is explained in terms of other concepts. For example:
C := A + B explains C in terms of A and B and +. Being talked ABOUT is equivalent to appearing on the left side of an assignment expression.
Once a concept has been derived (= talked ABOUT) within the discourse (= diagram) D,
it can be used to talk WITH, i.e., it can be used to help to explain other concepts within D.
Hence, derived concepts must be talked ABOUT (= introduced = defined = explained) before they can be talked WITH. When they have been talked ABOUT, they can be used to talk WITH (= in terms of) in order to talk ABOUT (= derive) other concepts.
1.7. Intentional versus extensional semantics
1.7.1 Intentional (≈ theoretical) aspect of a concept:
The definition of a concept expresses its intention, i.e., which properties it wants to express and delimit with respect to its surroundings.
We say that a concept can be applied to a certain object (= instance = example) of a concept if this object fulfills the intention of the concept, i.e., if the object satisfies the conditions (= has the properties) specified in the definition of the concept.
1.7.2 Extensional (≈ practical) aspect of a concept:
The set of objects that belong to a concept are called the concept’s extension (= examples = instances = entities).
1.8. Collectivation = Collective Learning = Raising the Collective Intelligence
Collective Conceptualization (= Collaborative Concept Formation) within a certain \, D_{iscourse} = C_{ontext} = D_{iagram} \, is driven by the MISMATCH of the \, D_{iscourse} , which is the SYMMETRIC DIFFERENCE \, I_{ntentions}(D_{iscourse}) \, \Delta \, E_{xtensions}(D_{iscourse}) \, between the \, I_{ntentions} = P_{roperties} \, (“property cluster”) and the \, E_{xtensions} = E_{xamples} \, (“object cluster”) that satisfy (= fit within = match) the (context of the) \, D_{iscourse} .
By collaboratively updating the \, I_{ntentions} \, and \, E_{xtensions} \, of the \, D_{iscourse} ,
its mismatch \, M = I \, \Delta \, E \, is affected.
The aim is to eliminate the mismatch of the discourse and arrive at \, I \, \Delta \, E = \emptyset \, ,
in which case all \, E_{xtensions} \, within this \, D_{iscourse} \, have been described by \, I_{ntentions} \, and no \, I_{ntention} \, is superfluous (= redundant) or contradictory (= empty = has no examples).
1.9. Formal Concept Analysis
Formal Concept Analysis (FCA) provides a principled way of automatically deriving an ontology from a collection of objects and their properties. The term was introduced by Rudolf Wille in 1984, and builds on applied lattice and order theory that was developed by Birkhoff and others in the 1930’s.
/////// Wikipedia provides the following intuitive description of FCA:
FCA refers to both an unsupervised machine learning technique and, more broadly, a method of data analysis. The approach takes as input a matrix specifying a set of objects and the properties thereof (also called attributes), and finds both all the “natural” clusters of properties and all the “natural” clusters of objects in the input data, where
• a ‘natural’ object cluster is the set of all objects that share a common subset of properties, and
• a ‘natural’ property cluster is the set of all properties shared by one of the natural object clusters.
Natural property clusters correspond one-for-one with natural object clusters, and a concept is a pair containing both a natural property cluster and its corresponding natural object cluster. The family of these concepts obeys the mathematical axioms defining a lattice, and is called a concept lattice. In French this is called a “Treillis de Galois” because the relation between the sets of concepts and attributes is a Galois connection.
This implies (among other things) that:
• Union(Properties) corresponds to Intersection(Objects), and
• Intersection(Properties) corresponds to Union(Objects).
/////// End of quote from Wikipedia
The interplay between properties (≈ constraints) and examples (≈ models)
1.5. The category of contoured contexts
Given two contoured contexts and , they induce a smallest inclusive contoured context as well as a largest common contoured context. The smallest inclusive context is called (for supremum) and the largest common context is called (for infimum). An ordered set, where supremum and infimum exist for any pair of members, is called a lattice.
////// Contexts have preorders that induce categories (Spivak, 2014, p. 244)
As is easily seen, any set of contoured contexts, ordered by inclusion, forms a lattice under union and intersection. This lattice is embedded in the powerset category of all subsets of the elements of a contoured context. [Note that in this model, a context is just a set.]
///////