This page is a sub-page of our page on Music.
///////
Related KMR-pages:
• Pythagorean Intervals
• The Logarithmic Piano
• Solfege: An Abstract Key System
• Chord Ladder
• Chord-Set Inclusion Graph
• Instantiations of Solfege in Different Keys
///////
Other relevant sources of information:
Swedish:
• Intervall
• Tonarter
• Ackord
• Skalor
• Pentatoniska skalor
• Kyrkotonarter
• Blues
• Skalafinnaren: bluesskalan
• Tonfrekvenser
• Övertoner
English:
• International Chorus Bulletin
• Staff (music)
• Clef (music)
• Cadence (music)
• The V-IV-I turnaround
• How Distortion works in Music
• How to Imitate a Whole Lot of Hollywood Film Music In Four Easy Steps
• How to Imitate Even More Closely a Whole Lot of Hollywood Film Music with One More Easy Step
///////
/////// Quoting from the International Chorus Bulletin:
A common misunderstanding of the “movable \, d_o ” system is that the tonic note is always called \, d_o . This opinion, held by many poorly informed critics of the system, is likely responsible for the erroneous belief that “movable \, d_o ” is not suited to “complex” music.
In order to unburden ourselves of this error, it should be made clear that, in the “movable \, d_o ” system, the names do not impose any hierarchy with respect to scale degrees. In other words, the solfa names are nothing more than reminders of the intervallic relationships between the various notes. To put this another way, one need only generate the seven well-known modes, as follows:
Scale type \qquad \qquad \, Tonic note (Note “#1”)
“Major” (Ionian) \qquad \qquad d_o \,
Dorian \qquad \qquad \qquad \quad \; r_e \,
Phrygian \qquad \qquad \qquad \; m_i \,
Lydian \qquad \qquad \qquad \quad \, f_a \,
Mixolydian \qquad \qquad \quad \;\;\, s_o \,
“Minor” (Aeolian) \qquad \quad \;\; l_a \,
Locrian \qquad \qquad \qquad \quad t_i \,
What we see above is that, for one thing, the “natural minor” scale, i.e., the official “relative minor”, uses \, l_a \, as its tonic. Even for individuals raised more or less exclusively on a diet of major-minor music, it can require some mental discipline to hear \, l_a \, as the tonic note, and to hear \, d_o \, as the minor third of that scale. Beyond these two, basic to most students whose experience with the Western tradition is often confined to music written post-1700, the remaining modes may require even more substantial perceptual overhauls at the outset. For instance, in the Phrygian scale, \, d_o \, functions as the flattened sixth degree, and so on.
/////// End of Quote from the International Chorus Bulletin.
///////
Church keys (Kirchentonarten):
[ \, d_{iatonic}s_{cale} \, ]_{I_{onian}} = \, \begin{matrix} \langle \, d_o & r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & l_a & \textcolor{red} {t_i} & \textcolor{red} {2 d_o} \, { \rangle }_{I_{onian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{D_{orian}} = \, \begin{matrix} \langle \, r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & l_a & \textcolor{red} {t_i} & \textcolor{red} {d_o} & 2 r_e \, { \rangle }_{D_{orian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{P_{hrygian}} = \, \begin{matrix} \langle \, \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & l_a & \textcolor{red} {t_i} & \textcolor{red} {d_o} & r_e & 2 m_i \, { \rangle }_{P_{hrygian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{L_{ydian}} = \, \begin{matrix} \langle \, f_a & s_o & l_a & \textcolor{red} {t_i} & \textcolor{red} {d_o} & r_e & \textcolor{red} {m_i} & \textcolor{red} {2 f_a} \, { \rangle }_{L_{ydian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{M_{ixoLydian}} = \, \begin{matrix} \langle \, s_o & l_a & \textcolor{red} {t_i} & \textcolor{red} {d_o} & r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & 2 s_o \, { \rangle }_{M_{ixoLydian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{A_{eolian}} = \, \begin{matrix} \langle \, l_a & \textcolor{red} {t_i} & \textcolor{red} {d_o} & r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & 2 l_a \, { \rangle }_{A_{eolian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{L_{ocrian}} = \, \begin{matrix} \langle \, \textcolor{red} {t_i} & \textcolor{red} {d_o} & r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & l_a & 2 t_i \, { \rangle }_{L_{ocrian}} \, \end{matrix} \,///////
CordLadder-peeking-into-the-Pentatonic-Melody-layer:
The Pentatonic-Melody-layer:
///////
The \, h_{armony} \dashv m_{elody} \, relationships between \, H_{armonic} \, and \, M_{elodic} \; S_{ub}S_{paces} \,
///////
\, \begin{matrix} X & {\xrightarrow{\;\;\;\;\;\;\;\;\;\;\;\;\; f \;\;\;\;\;\;\;\;\;\;\;\;\;}} & Y \\ {\uparrow \in} & & {\uparrow \in} \\ x & {\xmapsto{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} } & f(x) \end{matrix} \,NOTATION: In this diagram, the vertical arrows represent the memberships of the objects named at the bottom of an arrow in the set named at the top of the same arrow. Hence the vertical arrows tell us that \, x \in X \, and \, f(x) \in Y .
///////
\, \begin{matrix} H_{armonic}S_{ub}S_{pace} & {\xmapsto{\;\;\;\;\;\;\;\;\;\;\;\;\; m_{elody}(c_{hord}s_{equence}) \;\;\;\;\;\;\;\;\;\;\;\;\;}} & s_{ection}(M_{elodic}S_{ub}S_{pace}(c_{hord}s_{equence})) \\ & & & & \\ {\uparrow \in} & & \upuparrows \\ & & & & \\ c_{hord}s_{equence} & {\xmapsto{\, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} } & M_{elodic}S_{ub}S_{pace}(c_{hord}s_{equence}) \end{matrix} \,NOTATION: The section is represented by the double-vertical arrow to the right.
Saying that this diagram is commutative is the same as saying that:
\, m_{elody}(c_{hord}s_{equence}) \, = \, s_{ection}(M_{elodic}S_{ub}S_{pace}(c_{hord}s_{equence})) .
a_Melody (a_Chord_Sequence) is a section created by selection of which_Note_Sequence to play in harmony with the_Chord_Sequence, how to “rhythmify” this_Note_Sequence as well as how to “bend” its notes (≈ how to “approach” them ≈ how to “tweak” them) dynamically.
///////
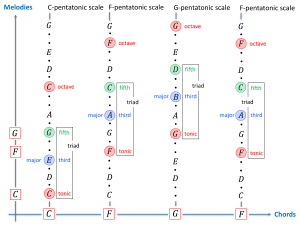
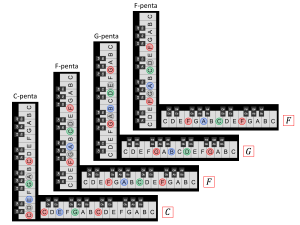
Melodic_Spaces of Concrete and Abstract Chord_Sequences
Concrete Chord Sequence: ||: \, C \, F \, G \, F \, :||
• La Bamba (Trini Lopez)
\, p_{entatonic}{\textcolor{red}{C}}_{scale} \, = \, \textcolor{red}{C} \, D \, \textcolor{blue}{E} \, \textcolor{green}{G} \, A \,
\, p_{entatonic}{\textcolor{red}{F}}_{scale} \, = \, \textcolor{red}{F} \, G \, \textcolor{blue}{A} \, \textcolor{green}{C} \, D \,
\, p_{entatonic}{\textcolor{red}{G}}_{scale} \, = \, \textcolor{red}{G} \, A \, \textcolor{blue}{B} \, \textcolor{green}{D} \, E \,
\, h_{armonic}{\textcolor{red}{C}}_{triad} \, = \, \textcolor{red}{C} \, \textcolor{blue}{E} \, \textcolor{green}{G} \,
\, h_{armonic}{\textcolor{red}{F}}_{triad} \, = \, \textcolor{red}{F} \, \textcolor{blue}{A} \, \textcolor{green}{C} \,
\, h_{armonic}{\textcolor{red}{G}}_{triad} \, = \, \textcolor{red}{G} \, \textcolor{blue}{B} \, \textcolor{green}{D} \,
A melody as a pentatonic section of a diatonic harmony sequence
A pentatonic melody sequence
over each chord of
a diatonic harmony sequence
///////
\, H_{armony}B_{ased}M_{usic} \, = \, {\bigoplus \atop {h_{armonies} } } ( \, m_{elodies} \, \mathbf{R} \, h_{armony} \, ) \, = \,\, = \, {\bigoplus \atop {h_{armonies} } } \, ( \, {\bigoplus \atop {m_{elodies} } } \, ( \, m_{elody}\, \mathbf{R} \, h_{armony} \, ) \, ) \, .
\, M_{elody}B_{ased}M_{usic} \, = \, {\bigoplus \atop {m_{elodies} } } \, ( \, m_{elody} \, \mathbf{R} \, h_{armonies} \, ) \, = \,\, = \, {\bigoplus \atop {m_{elodies} } } \, ( \, {\bigoplus \atop {h_{armonies} } } \, ( \, m_{elody} \, \mathbf{R} \, h_{armony} \, ) \, ) \, .
///////
\, [ \, h_{armony} \, ]_{M_{usic}} \, \mapsto \, \left< \, c_{hord}s_{equences} \, \mathrm{based \, on} \; s_{cales} \, \right>_{M_{usic}} \, \, [ \, m_{elody} \, ]_{M_{usic}} \, \mapsto \, \left< \, t_{ropes} \, \mathrm{based \, on} \; s_{cales} \, \right>_{M_{usic}} \,///////
\, [ \, h_{armony} \, ]_{P_{opular} \, M_{usic}} \, \mapsto \, \left< \, c_{hord}s_{equences} \, \mathrm{based \, on} \; d_{iatonic} \, s_{cales} \, \right>_{P_{opular} \, M_{usic}} \, [ \, m_{elody} \, ]_{P_{opular} \, M_{usic}} \, \mapsto \, \left< \, t_{ropes} \, \mathrm{based \, on} \; p_{entatonic} \, s_{cales} \, \right>_{P_{opular} \, M_{usic}}///////
• Musical scale
• Musical trope
• Popular music
• Diatonic scale
• Pentatonic scale
• Modal frame = Melodic mode
• Tonality
• Atonality
///////
///////
Transposition of the ||: \, C \, F \, G \, F \, :|| chord sequence:
Changing the key from \, C \, to \, F \, gives the
Concrete Chord Sequence: ||: \, F \, B_b \, C \, B_b \, :||
• Twist and Shout (Isley Brothers)
and transposing any one of these representations to the key of \, D \, gives the
Concrete Chord Sequence: ||: \, D \, G \, A \, G \, :||
• Twist and Shout (The Beatles)
///////
The three concrete chord sequences listed above all conform to the same
Abstract Chord Sequence: ||: \, d_o \, f_a \, s_o \, f_a \, :||
\, p_{entatonic}{\textcolor{red}{d_o}}s_{cale} \, = \, \textcolor{red}{d_o} \, r_e \, \textcolor{blue}{m_i} \, \textcolor{green}{s_o} \, l_a \,
\, p_{entatonic}{\textcolor{red}{f_a}}s_{cale} \, = \, \textcolor{red}{f_a} \, s_o \, \textcolor{blue}{l_a} \, \textcolor{green}{d_o} \, r_e \,
\, p_{entatonic}{\textcolor{red}{s_o}}s_{cale} \, = \, \textcolor{red}{s_o} \, l_a \, \textcolor{blue}{t_i} \, \textcolor{green}{r_e} \, m_i \,
\, h_{armonic}{\textcolor{red}{d_o}}t_{riad} \, = \, \textcolor{red}{d_o} \, \textcolor{blue}{m_i} \, \textcolor{green}{s_o} \,
\, h_{armonic}{\textcolor{red}{f_a}}t_{riad} \, = \, \textcolor{red}{f_a} \, \textcolor{blue}{l_a} \, \textcolor{green}{d_o} \,
\, h_{armonic}{\textcolor{red}{s_o}}t_{riad} \, = \, \textcolor{red}{s_o} \, \textcolor{blue}{t_i} \, \textcolor{green}{r_e} \,
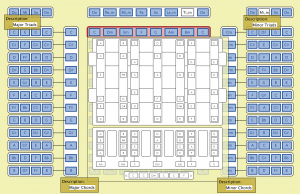
The Pentatonic_Melody_Space over the ||: \, d_o \, f_a \, s_o \, f_a \, :|| Chord_Sequence:
The melody of a pentatonic tune “lives” within the pentatonic scales of the chord-sequence that supports the harmony of the tune. When a chord of this sequence is active (= sounding) the melody must remain within the pentatonic scale of this chord – but it is free to vary its melodic sequence of notes with respect to both pitch and rhythm. When the chord changes, the melody must “roll itself out” within the pentatonic scale of the new chord as long as the latter is active.
///////
Queen Jane Approximately (harmonies and melody-possibilities):
• Queen Jane Approximately (D) by Bob Dylan + impro piano overlay by Ambjörn Naeve.
///////
• Ackord (in Swedish)
///////
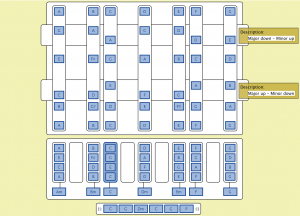
The Pentatonic melody space over the Twelve-bar Blues chord sequence:
///////
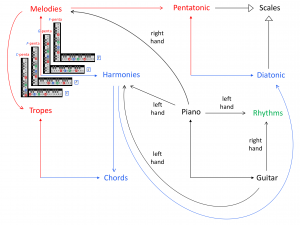
Piano and Guitar in Harmonies, Melodies and Rhythms:
///////
More examples of improvisation piano overlays (by Ambjörn Naeve):
• Little House On The Hill (E) by Willie Nelson.
• Fame (A) by Van Morrison.
• Just Like Tom Thumb’s Blues (E) by Bob Dylan.
• Something There Is About You (G) by Bob Dylan.
• Knockin’ On Heaven’s Door (G) by Bob Dylan (with Mark Knopfler).
• Positively Fourth Street (G) by Bob Dylan.
• The Times They Are a’ Changin’ (A) by Bob Dylan.
• Love Minus Zero – No Limits (C) by Bob Dylan.
• These Days (F) by Jackson Browne.
• Lady Of The Well (G) by Jackson Browne.
• Takin’ It Easy (G) by Jackson Browne.
///////
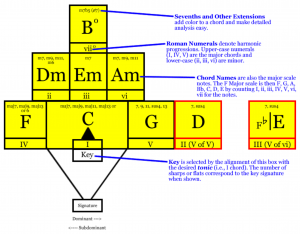
The chord ladder:
/////// Chords:
• Ackord
///////
NOTATION: \, H \, is also denoted by \, B \, .
///////
///////
///////
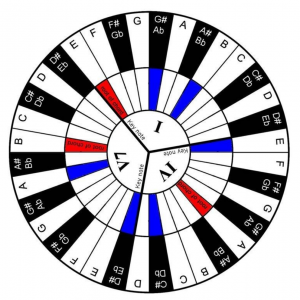
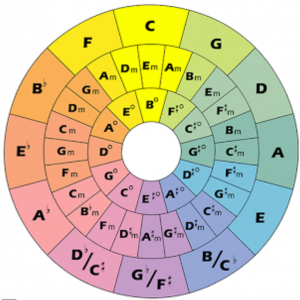
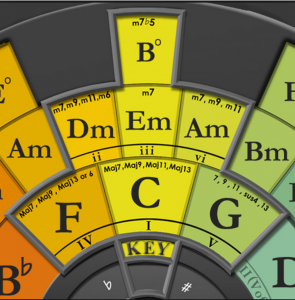
A chord wheel for piano
(Structurally, this is a slide rule “wrapped around three octaves”):
///////
The Chord Wheel:
///////
///////
The Pentatonic_Melody_Space over the Chord_Ladder_Sequence in the key of \, C :
Chord Ladder start: \; ( \, C \; D_m \; E_m \; F \, ) \;
Chord Ladder finish: \; ( \, G \; A_m \; B_m \; C \, ) \;
///////
/////// Quoting from Overview of pentatonic scales in music theory
Major and Minor Pentatonic Scales:
The two basic forms of pentatonic scales are major and minor. The major scale consists of the first – second – third – fifth – sixth notes of a major scale.
The minor notes consist of the same five notes of a major pentatonic scale but its tonic (first note of the scale) is three semitones below the tonic of the major pentatonic scale. For example, the C major pentatonic (C – D – E – G – A) has the same notes as the A minor pentatonic (A – C – D – E – G) but arranged differently. The first note or tonic of the A minor pentatonic scale (= A) is three semitones (half steps) lower than the first note of the C major pentatonic scale (= C). It uses the first – minor third – fourth – fifth – minor seventh notes of a scale.
/////// End of Quote
The major pentatonic scales:
\, \begin{matrix} \textcolor{red}{C} & D & \textcolor{blue}{E} & \textcolor{green}{G} & A & \textcolor{red}{C} \\ \;\;\,{\textcolor{red}{C^{\#}}} & \;\;\,D^{\#} & \textcolor{blue}{F} & \;\;\,{\textcolor{green}{G^{\#}}} & \;B_b & \;\;\,{\textcolor{red}{C^{\#}}} \\ \textcolor{red}{D} & E & \;\;\,{\textcolor{blue}{F^{\#}}} & {\textcolor{green}{A}} & B & \textcolor{red}{D} \\ \;\;\,{\textcolor{red}{D^{\#}}} & F & \textcolor{blue}{G} & \;{\textcolor{green}{B_b}} & C & \;\;{\textcolor{red}{D^{\#}}} \\ \textcolor{red}{E} & \;\;\,F^{\#} & \;\;\,{\textcolor{blue}{G^{\#}}} & {\textcolor{green}{B}} & \;\;\,C^{\#} & \textcolor{red}{E} \\ \textcolor{red}{F} & G & \textcolor{blue}{A} & \textcolor{green}{C} & D & \textcolor{red}{F} \\ \;\;\,{\textcolor{red}{F^{\#}}} & \;\;\,G^{\#} & \;{\textcolor{blue}{B_b}} & \;\;\,{\textcolor{green}{C^{\#}}} & \;\;\,D^{\#} & \;\;\,{\textcolor{red}{F^{\#}}} \\ \textcolor{red}{G} & A & \textcolor{blue}{B} & \textcolor{green}{D} & E & \textcolor{red}{G} \\ \;\;\,{\textcolor{red}{G^{\#}}} & \;B_b & \textcolor{blue}{C} & \;\;\,{\textcolor{green}{D^{\#}}} & F & \;\;\,{\textcolor{red}{G^{\#}}} \\ \textcolor{red}{A} & B & \;\;\,{\textcolor{blue}{C^{\#}}} & \textcolor{green}{E} & \;\;\,F^{\#} & \textcolor{red}{A} \\ \;{\textcolor{red}{B_b}} & C & \textcolor{blue}{D} & \textcolor{green}{F} & G & \;{\textcolor{red}{B_b}} \\ \textcolor{red}{B} & \;\;\,C^{\#} & \;\;\,{\textcolor{blue}{D^{\#}}} & \;\;\,{\textcolor{green}{F^{\#}}} & \;\;\,G^{\#} & \textcolor{red}{B} \\ \textcolor{red}{C} & D & \textcolor{blue}{E} & \textcolor{green}{G} & A & \textcolor{red}{C} \end{matrix} \,///////
The minor pentatonic scales:
\, \begin{matrix} \textcolor{red}{C} & D & \;\;\,\textcolor{blue}{D^{\#}} & \textcolor{green}{G} & \;B_b & \textcolor{red}{C} \\ \;\;\,{\textcolor{red}{C^{\#}}} & \;\;\,D^{\#} & \textcolor{blue}{E} & \;\;\,{\textcolor{green}{G^{\#}}} & B & \;\;\,{\textcolor{red}{C^{\#}}} \\ \textcolor{red}{D} & E & \,{\textcolor{blue}{F}} & \textcolor{green}{A} & C & \textcolor{red}{D} \\ \;\;\,{\textcolor{red}{D^{\#}}} & F & \;\;\textcolor{blue}{F^{\#}} & \;{\textcolor{green}{B_b}} & \;\;C^{\#} & \;\;{\textcolor{red}{D^{\#}}} \\ \textcolor{red}{E} & \;\;\,F^{\#} & \textcolor{blue}{G} & {\textcolor{green}{B}} & D & \textcolor{red}{E} \\ \textcolor{red}{F} & G & \;\;{\textcolor{blue}{G^{\#}}} & \textcolor{green}{C} & \;\;D^{\#} & \textcolor{red}{F} \\ \;\;\,{\textcolor{red}{F^{\#}}} & \;\;\,G^{\#} & \textcolor{blue}{A} & \;\;\,{\textcolor{green}{C^{\#}}} & E & \;\;\,{\textcolor{red}{F^{\#}}} \\ \textcolor{red}{G} & A & \;{\textcolor{blue}{B_b}} & \textcolor{green}{D} & F & \textcolor{red}{G} \\ \;\;\,{\textcolor{red}{G^{\#}}} & \;B_b & \;\;\,{\textcolor{blue}{C^{\#}}} & \;\;\,{\textcolor{green}{D^{\#}}} & \;\;\,F^{\#} & \;\;\,{\textcolor{red}{G^{\#}}} \\ \textcolor{red}{A} & B & {\textcolor{blue}{C}} & \textcolor{green}{E} & G & \textcolor{red}{A} \\ \;{\textcolor{red}{B_b}} & C & \;\;{\textcolor{blue}{C^{\#}}} & \textcolor{green}{F} & \;\;G^{\#} & \;{\textcolor{red}{B_b}} \\ \textcolor{red}{B} & \;\;\,C^{\#} & \textcolor{blue}{D} & \;\;\,{\textcolor{green}{F^{\#}}} & A & \textcolor{red}{B} \\ \textcolor{red}{C} & D & \;\;\textcolor{blue}{D^{\#}} & \textcolor{green}{G} & \;B_b & \textcolor{red}{C} \end{matrix} \,///////
How the melody can determine the harmony
The key possibilities of the \, C D E \, melodic fragment:
\, \begin{matrix} & & & & & & & C & D & E \\ \textcolor{red}{C} & D & \textcolor{blue}{E} & \textcolor{green}{G} & A & \textcolor{red}{C} & & m_{aybe} & m_{aybe} & y_{es} \\ \;\;\,{\textcolor{red}{C^{\#}}} & \;\;\,D^{\#} & \textcolor{blue}{F} & \;\;\,{\textcolor{green}{G^{\#}}} & \;B_b & \;\;\,{\textcolor{red}{C^{\#}}} & & n_o & & & & \\ \textcolor{red}{D} & E & \;\;\,{\textcolor{blue}{F^{\#}}} & {\textcolor{green}{A}} & B & \textcolor{red}{D} & & n_o & & & & \\ \;\;\,{\textcolor{red}{D^{\#}}} & F & \textcolor{blue}{G} & \;{\textcolor{green}{B_b}} & C & \;\;{\textcolor{red}{D^{\#}}} & & m_{aybe} & n_o & & \\ \textcolor{red}{E} & \;\;\,F^{\#} & \;\;\,{\textcolor{blue}{G^{\#}}} & {\textcolor{green}{B}} & \;\;\,C^{\#} & \textcolor{red}{E} & & n_o & & & & \\ \textcolor{red}{F} & G & \textcolor{blue}{A} & \textcolor{green}{C} & D & \textcolor{red}{F} & & m_{aybe} & m_{aybe} & n_o \\ \;\;\,{\textcolor{red}{F^{\#}}} & \;\;\,G^{\#} & \;{\textcolor{blue}{B_b}} & \;\;\,{\textcolor{green}{C^{\#}}} & \;\;\,D^{\#} & \;\;\,{\textcolor{red}{F^{\#}}} & & n_o & & & & \\ \textcolor{red}{G} & A & \textcolor{blue}{B} & \textcolor{green}{D} & E & \textcolor{red}{G} & & n_o & & & & \\ \;\;\,{\textcolor{red}{G^{\#}}} & \;B_b & \textcolor{blue}{C} & \;\;\,{\textcolor{green}{D^{\#}}} & F & \;\;\,{\textcolor{red}{G^{\#}}} & & m_{aybe} & n_o & & \\ \textcolor{red}{A} & B & \;\;\,{\textcolor{blue}{C^{\#}}} & \textcolor{green}{E} & \;\;\,F^{\#} & \textcolor{red}{A} & & n_o & & & & \\ \;{\textcolor{red}{B_b}} & C & \textcolor{blue}{D} & \textcolor{green}{F} & G & \;{\textcolor{red}{B_b}} & & m_{aybe} & m_{aybe} & n_o \\ \textcolor{red}{B} & \;\;\,C^{\#} & \;\;\,{\textcolor{blue}{D^{\#}}} & \;\;\,{\textcolor{green}{F^{\#}}} & \;\;\,G^{\#} & \textcolor{red}{B} & & n_o & & & & \\ \textcolor{red}{C} & D & \textcolor{blue}{E} & \textcolor{green}{G} & A & \textcolor{red}{C} \end{matrix} \,The key is defined as the tonic of the supporting chord. The melodic sequence \, CDE \, is played and the impossible keys are successively eliminated “note-by-note” – until only one possibility remains.
The initial melodic note \, C \, appears in the five possible keys \, C, D^{\#}, F, G^{\#}, B_b \, and their pentatonic scales are indicated by \, m_{aybe} in the corresponding rows of the \, C -column of the above matrix.
The note \, C \, does NOT appear in the seven impossible (= non-compatible) keys \, C^{\#}, D, E, F^{\#}, G, A, B \, and their pentatonic scales are indicated by \, n_o in the corresponding rows of the \, C -column.
The next melodic note \, D \, eliminates two of the five \, C -possibilities, which leaves three \, CD -possibilities still open. They are indicated by \, m_{aybe} \, in the corresponding rows of the \, D -column.
The final melodic note \, E \, eliminates two of these three \, CD -possibilities, leaving only one \, CDE -possibility, namely the key of \, C . This is indicated by the \, y_{es} \, in the top row of the \, E -column, which corresponds to the key of \, C . The melody-fragment \, CDE \, must therefore be played in the key of \, C .
///////
The key possibilities of the \, C \, F \, G \, B_b \, melodic fragment:
\, \begin{matrix} & & & & & & & C & F & G & B_b \\ \textcolor{red}{C} & D & \textcolor{blue}{E} & \textcolor{green}{G} & A & \textcolor{red}{C} & & m_{aybe} & n_o \\ \;\;\,{\textcolor{red}{C^{\#}}} & \;\;\,D^{\#} & \textcolor{blue}{F} & \;\;\,{\textcolor{green}{G^{\#}}} & \;B_b & \;\;\,{\textcolor{red}{C^{\#}}} & & n_o & & & & \\ \textcolor{red}{D} & E & \;\;\,{\textcolor{blue}{F^{\#}}} & {\textcolor{green}{A}} & B & \textcolor{red}{D} & & n_o & & & & \\ \;\;\,{\textcolor{red}{D^{\#}}} & F & \textcolor{blue}{G} & \;{\textcolor{green}{B_b}} & C & \;\;{\textcolor{red}{D^{\#}}} & & m_{aybe} & m_{aybe} & m_{aybe} & m_{aybe} \\ \textcolor{red}{E} & \;\;\,F^{\#} & \;\;\,{\textcolor{blue}{G^{\#}}} & {\textcolor{green}{B}} & \;\;\,C^{\#} & \textcolor{red}{E} & & n_o & & & & \\ \textcolor{red}{F} & G & \textcolor{blue}{A} & \textcolor{green}{C} & D & \textcolor{red}{F} & & m_{aybe} & m_{aybe} & m_{aybe} & n_o \\ \;\;\,{\textcolor{red}{F^{\#}}} & \;\;\,G^{\#} & \;{\textcolor{blue}{B_b}} & \;\;\,{\textcolor{green}{C^{\#}}} & \;\;\,D^{\#} & \;\;\,{\textcolor{red}{F^{\#}}} & & n_o \\ \textcolor{red}{G} & A & \textcolor{blue}{B} & \textcolor{green}{D} & E & \textcolor{red}{G} & & n_o \\ \;\;\,{\textcolor{red}{G^{\#}}} & \;B_b & \textcolor{blue}{C} & \;\;\,{\textcolor{green}{D^{\#}}} & F & \;\;\,{\textcolor{red}{G^{\#}}} & & m_{aybe} & m_{aybe} & n_o \\ \textcolor{red}{A} & B & \;\;\,{\textcolor{blue}{C^{\#}}} & \textcolor{green}{E} & \;\;\,F^{\#} & \textcolor{red}{A} & & n_o \\ \;{\textcolor{red}{B_b}} & C & \textcolor{blue}{D} & \textcolor{green}{F} & G & \;{\textcolor{red}{B_b}} & & m_{aybe} & m_{aybe} & m_{aybe} & m_{aybe} \\ \textcolor{red}{B} & \;\;\,C^{\#} & \;\;\,{\textcolor{blue}{D^{\#}}} & \;\;\,{\textcolor{green}{F^{\#}}} & \;\;\,G^{\#} & \textcolor{red}{B} & & n_o \\ \textcolor{red}{C} & D & \textcolor{blue}{E} & \textcolor{green}{G} & A & \textcolor{red}{C} \end{matrix} \,///////
The key possibilities of the \, C D G \, melodic fragment:
\, \begin{matrix} & & & & & & & C & D & G \\ \textcolor{red}{C} & D & \textcolor{blue}{E} & \textcolor{green}{G} & A & \textcolor{red}{C} & & m_{aybe} & m_{aybe} & m_{aybe} \\ \;\;\,{\textcolor{red}{C^{\#}}} & \;\;\,D^{\#} & \textcolor{blue}{F} & \;\;\,{\textcolor{green}{G^{\#}}} & \;B_b & \;\;\,{\textcolor{red}{C^{\#}}} & & n_o & & & & \\ \textcolor{red}{D} & E & \;\;\,{\textcolor{blue}{F^{\#}}} & {\textcolor{green}{A}} & B & \textcolor{red}{D} & & n_o & & & & \\ \;\;\,{\textcolor{red}{D^{\#}}} & F & \textcolor{blue}{G} & \;{\textcolor{green}{B_b}} & C & \;\;{\textcolor{red}{D^{\#}}} & & m_{aybe} & n_o \\ \textcolor{red}{E} & \;\;\,F^{\#} & \;\;\,{\textcolor{blue}{G^{\#}}} & {\textcolor{green}{B}} & \;\;\,C^{\#} & \textcolor{red}{E} & & n_o \\ \textcolor{red}{F} & G & \textcolor{blue}{A} & \textcolor{green}{C} & D & \textcolor{red}{F} & & m_{aybe} & m_{aybe} & m_{aybe} \\ \;\;\,{\textcolor{red}{F^{\#}}} & \;\;\,G^{\#} & \;{\textcolor{blue}{B_b}} & \;\;\,{\textcolor{green}{C^{\#}}} & \;\;\,D^{\#} & \;\;\,{\textcolor{red}{F^{\#}}} & & n_o \\ \textcolor{red}{G} & A & \textcolor{blue}{B} & \textcolor{green}{D} & E & \textcolor{red}{G} & & n_o \\ \;\;\,{\textcolor{red}{G^{\#}}} & \;B_b & \textcolor{blue}{C} & \;\;\,{\textcolor{green}{D^{\#}}} & F & \;\;\,{\textcolor{red}{G^{\#}}} & & m_{aybe} & n_o \\ \textcolor{red}{A} & B & \;\;\,{\textcolor{blue}{C^{\#}}} & \textcolor{green}{E} & \;\;\,F^{\#} & \textcolor{red}{A} & & n_o \\ \;{\textcolor{red}{B_b}} & C & \textcolor{blue}{D} & \textcolor{green}{F} & G & \;{\textcolor{red}{B_b}} & & m_{aybe} & m_{aybe} & m_{aybe} \\ \textcolor{red}{B} & \;\;\,C^{\#} & \;\;\,{\textcolor{blue}{D^{\#}}} & \;\;\,{\textcolor{green}{F^{\#}}} & \;\;\,G^{\#} & \textcolor{red}{B} & & n_o \\ \textcolor{red}{C} & D & \textcolor{blue}{E} & \textcolor{green}{G} & A & \textcolor{red}{C} \end{matrix} \,///////
The visual appearance of the Major Third in Pythagorean tuning
The counting is based on the diatonic scale: \, d_o, r_e, m_i, f_a, s_o, l_a, t_i, 2 d_o . The first note, \, d_o , is depicted in purple, the third note, \, m_i , is depicted in light-blue, and the sum of these two notes, \, d_o + m_i , i.e., the Major Third, is depicted in black.
Frequency ratio: \, m_i/d_o = 5/4 .
NOTE: The Wikipedia page on the musical interval called the major third contains an important error. In the second paragraph of the introduction it states that:
“The major third may be derived from the harmonic series
as the interval between the fourth and fifth harmonics.”
This is not true. In fact,
in pythagorean tuning (= just intonation) we have:
\, q_{uart} \, * \, m_{ajor}t_{hird} \, = \, \frac{4}{3} \, * \, \frac{5}{4} \, = \, \frac{5}{3} \, \neq \, q_{uint} \, = \, \frac{3}{2} .
It is not the interval of a major third but the interval of a second that works as the multiplier that transforms the quart into the quint. The reason for this is that in pythagorean tuning we have:
\, q_{uart} \, * \, s_{econd} \, = \, \frac{4}{3} \, * \, \frac{9}{8} \, = \, \frac{3}{2} \, = \, q_{uint} ,
and in equally tempered tuning we have:
\, q_{uart} \, * \, s_{econd} \, = \, 2^{\, \frac{5}{12}} \, * \, 2^{\, \frac{2}{12}} \, = \, 2^{\, \frac{5+2}{12}} \, = \, 2^{\, \frac{7}{12}} \, = \, q_{uint} .
///////
The visual appearance of the Quart (= Fourth) in Pythagorean tuning
The counting is based on the diatonic scale: \, d_o, r_e, m_i, f_a, s_o, l_a, t_i, 2 d_o . The first note, \, d_o , is depicted in purple, the fourth note, \, f_a , is depicted in light-blue, and the sum of these two notes, \, d_o + f_a , i.e., the Quart, is depicted in black.
Frequency ratio: \, f_a/d_o = 4/3 .
///////
The visual appearance of the Quint (= Fifth) in Pythagorean tuning
The counting is based on the diatonic scale: \, d_o, r_e, m_i, f_a, s_o, l_a, t_i, 2 d_o . The first note, \, d_o , is depicted in purple, the fifth note, \, s_o , is depicted in light-blue, and the sum of these two notes, \, d_o + s_o , i.e., the Quint, is depicted in black.
Frequency ratio: \, s_o/d_o = 3/2 .
///////
The Quint and its Fourier Series:
The Fourier Series of the Quint is depicted in the window to the right. It consists of three terms, and it is therefore of the form \, F_1 sin(x) + F_2 sin(2x) + F_3 sin(3x) \, where \, F_1, F_2, F_3 \, are the respective Fourier coefficients of the wave. The tonic note is depicted in purple.
NOTE: The quint in the right window is generated with a tonic whose pitch is an octave higher than the pitch of the tonic depicted in the left window . This is because the tonic note in the left window is generated as the standing wave where \, y(x) = sin(x-2πn) + sin(x+2πn) \, with pitch \, d_o .
In contrast, the tonic note in the right window is generated as \, y(x) = F_1 sin(x) + F_2 sin(2x) \, where \, F_1 \, and \, F_2 \, are the first and the second Fourier-coefficients of the Quint. Since the pitch of a standing wave is proportional to its frequency, the \, d_o -tonic to the right has the pitch \, 2 d_o \, which is twice the pitch of the \, d_o -tonic to the left.
///////
The visual appearance of the Major Triad in Pythagorean tuning
The counting is based on the diatonic scale: \, d_o, r_e, m_i, f_a, s_o, l_a, t_i, 2 d_o . The first note, \, d_o , is depicted in purple, the third note, \, m_i , is depicted in light-blue, the fifth note, \, s_o , is depicted in green, and the sum of these notes, \, d_o + m_i + s_o , i.e., the Major Triad, is depicted in black.
Frequency ratios: \, m_i/d_o = 5/4 \, and \, s_o/d_o = 3/2 .
Church keys (Kirchentonarten):
[ \, d_{iatonic}s_{cale} \, ]_{I_{onian}} = \, \begin{matrix} \langle \, d_o & r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & l_a & \textcolor{red} {t_i} & \textcolor{red} {2 d_o} \, { \rangle }_{I_{onian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{D_{orian}} = \, \begin{matrix} \langle \, r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & l_a & \textcolor{red} {t_i} & \textcolor{red} {d_o} & 2 r_e \, { \rangle }_{D_{orian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{P_{hrygian}} = \, \begin{matrix} \langle \, \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & l_a & \textcolor{red} {t_i} & \textcolor{red} {d_o} & r_e & 2 m_i \, { \rangle }_{P_{hrygian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{L_{ydian}} = \, \begin{matrix} \langle \, f_a & s_o & l_a & \textcolor{red} {t_i} & \textcolor{red} {d_o} & r_e & \textcolor{red} {m_i} & \textcolor{red} {2 f_a} \, { \rangle }_{L_{ydian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{M_{ixoLydian}} = \, \begin{matrix} \langle \, s_o & l_a & \textcolor{red} {t_i} & \textcolor{red} {d_o} & r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & 2 s_o \, { \rangle }_{M_{ixoLydian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{A_{eolian}} = \, \begin{matrix} \langle \, l_a & \textcolor{red} {t_i} & \textcolor{red} {d_o} & r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & 2 l_a \, { \rangle }_{A_{eolian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{L_{ocrian}} = \, \begin{matrix} \langle \, \textcolor{red} {t_i} & \textcolor{red} {d_o} & r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & l_a & 2 t_i \, { \rangle }_{L_{ocrian}} \, \end{matrix} \,///////
Major and Minor Diatonic Scales:
Since \, I_{onian} = M_{ajor} \, and \, A_{eolian} = M_{inor} \, we have the following representations of the diatonic major (= “dur”) and diatonic minor (= “moll”) scales:
[ \, d_{iatonic}s_{cale} \, ]_{I_{onian}} = \, \begin{matrix} \langle \, m_{ajor}d_{iatonic}s_{cale} { \rangle }_{I_{onian}} \, \end{matrix} = \, \begin{matrix} \langle \, d_o & r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & l_a & \textcolor{red} {t_i} & \textcolor{red} {2 d_o} \, { \rangle }_{I_{onian}} \, \end{matrix} \, [ \, d_{iatonic}s_{cale} \, ]_{A_{eolian}} = \, \begin{matrix} \langle \, m_{inor}d_{iatonic}s_{cale} { \rangle }_{A_{eolian}} \, \end{matrix} = \, \begin{matrix} \langle \, l_a & \textcolor{red} {t_i} & \textcolor{red} {d_o} & r_e & \textcolor{red} {m_i} & \textcolor{red} {f_a} & s_o & 2 l_a \, { \rangle }_{A_{eolian}} \, \end{matrix} \,To transpose the minor diatonic scale from the tonic \, l_a \, to the tonic \, d_o \, we can shift it three half-tone steps upwards (= towards the right on the piano). We then get:
[ \, d_{iatonic}s_{cale} \, ]_{A_{eolian}} = \, \begin{matrix} \langle \, m_{inor}d_{iatonic}s_{cale} { \rangle }_{A_{eolian}} \, \end{matrix} = \, \begin{matrix} \langle \, d_o & \textcolor{red} {r_e} & \textcolor{red} {{r_e}^{\#}} & f_a & \textcolor{red}{s_o} & \textcolor{red} {{s_o}^{\#}} & {{t_i}_b} & 2 d_o \, { \rangle }_{A_{eolian}} \, \end{matrix} \,Note: The two half-tone intervals of the shifted scale still appear in positions 2-3 and 5-6.
///////
[ \, p_{entatonic}s_{cale} \, ]_{M_{ajor}} = \, \begin{matrix} \langle \, \textcolor{red}{d_o} & r_e & \textcolor{blue}{m_i} & \textcolor{green}{s_o} & l_a & \textcolor{red}{2 d_o} \, { \rangle }_{M_{ajor}} \, \end{matrix} \, [ \, p_{entatonic}s_{cale} \, ]_{M_{inor}} = \, \begin{matrix} \langle \, \textcolor{red}{d_o} & r_e & \textcolor{blue}{{r_e}^{\#}} & \textcolor{green}{s_o} & {{t_i}_b} & \textcolor{red}{2 d_o} \, { \rangle }_{M_{inor}} \, \end{matrix} \,///////
[ \, m_{inor}s_{econd} \, ]_{M_{ajor} o_r M_{inor}} = \, \begin{matrix} \langle \, m_{inor}s_{econd} \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} = \, \begin{matrix} \langle \, d_o \, {d_o}^{\#} \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} \, [ \, m_{ajor}s_{econd} \, ]_{M_{ajor} o_r M_{inor}} = \, \begin{matrix} \langle \, m_{ajor}s_{econd} \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} = \, \begin{matrix} \langle \, d_o \, r_e \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} \, [ \, m_{inor}t_{hird} \, ]_{M_{ajor} o_r M_{inor}} = \, \begin{matrix} \langle \, m_{inor}t_{hird} \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} = \, \begin{matrix} \langle \, d_o \, {r_e}^{\#} \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} \, [ \, m_{ajor}t_{hird} \, ]_{M_{ajor} o_r M_{inor}} = \, \begin{matrix} \langle \, m_{ajor}t_{hird} \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} = \, \begin{matrix} \langle \, d_o \, m_i \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} \, [ \, f_{ourth} \, ]_{M_{ajor} o_r M_{inor}} = \, \begin{matrix} \langle \, f_{ourth} \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} \, = \, \begin{matrix} \langle \, d_o \, f_a \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} \, [ \, f_{ifth} \, ]_{M_{ajor} o_r M_{inor}} = \, \begin{matrix} \langle \, f_{ifth} \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} \, = \, \begin{matrix} \langle \, d_o \, s_o \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} \, [ \, o_{ctave} \, ]_{M_{ajor} o_r M_{inor}} = \, \begin{matrix} \langle \, o_{ctave} \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} = \, \begin{matrix} \langle \, d_o \, 2 d_o \, { \rangle }_{M_{ajor} o_r M_{inor}} \, \end{matrix} \,///////
[ \, f_{requency}(u_{nison}) \, ]_{P_{ythagorean}} \, = \, [ \, f_{requency}(d_o \, d_o) \, ]_{P_{ythagorean}} = \, \begin{matrix} \langle \, \frac {1}{1} \, { \rangle }_{P_{ythagorean}} \, \end{matrix} \, [ \, f_{requency}(m_{inor}s_{econd}) \, ]_{P_{ythagorean}} \, = \, [ \, f_{requency}(d_o \, {d_o}^{\#}) \, ]_{P_{ythagorean}} = \, \begin{matrix} \langle \, \frac {16}{15} \, { \rangle }_{P_{ythagorean}} \, \end{matrix} \, [ \, f_{requency}(m_{ajor}s_{econd}) \, ]_{P_{ythagorean}} \, = \, [ \, f_{requency}(d_o \, r_e) \, ]_{P_{ythagorean}} \, = \, \begin{matrix} \langle \, \frac {9}{8} \, { \rangle }_{P_{ythagorean}} \, \end{matrix} \, [ \, f_{requency}(m_{inor}t_{hird}) \, ]_{P_{ythagorean}} = \, [ \, f_{requency}(d_o \, {r_e}^{\#}) \, ]_{P_{ythagorean}} \, = \, \begin{matrix} \langle \, \frac {6}{5} \, { \rangle }_{P_{ythagorean}} \, \end{matrix} \, [ \, f_{requency}(m_{ajor}t_{hird}) \, ]_{P_{ythagorean}} = \, [ \, f_{requency}(d_o \, m_i) \, ]_{P_{ythagorean}} \, = \, \begin{matrix} \langle \, \frac {5}{4} \, { \rangle }_{P_{ythagorean}} \, \end{matrix} \, [ \, f_{requency}(f_{ourth}) \, ]_{P_{ythagorean}} = \, [ \, f_{requency}(d_o \, f_a) \, ]_{P_{ythagorean}} \, = \, \begin{matrix} \langle \, \frac {4}{3} \, { \rangle }_{P_{ythagorean}} \, \end{matrix} \, [ \, f_{requency}(f_{ifth}) \, ]_{P_{ythagorean}} = \, [ \, f_{requency}(d_o \, s_o) \, ]_{P_{ythagorean}} \, = \, \begin{matrix} \langle \, \frac {3}{2} \, { \rangle }_{P_{ythagorean}} \, \end{matrix} \, [ \, f_{requency}(o_{ctave}) \, ]_{P_{ythagorean}} = \, [ \, f_{requency}(d_o \, 2 d_o) \, ]_{P_{ythagorean}} \, = \, \begin{matrix} \langle \, \frac {2}{1} \, { \rangle }_{P_{ythagorean}} \, \end{matrix} \,///////
[ \, f_{requency}(u_{nison}) \, ]_{T_{empered}} \, = \, [ \, f_{requency}(d_o \, d_o) \, ]_{T_{empered}} = \, \begin{matrix} \langle \, 2^{\, \frac{0}{12}} \, { \rangle }_{T_{empered}} \, \end{matrix} \, [ \, f_{requency}(m_{inor}s_{econd}) \, ]_{T_{empered}} \, = \, [ \, f_{requency}(d_o \, {d_o}^{\#}) \, ]_{T_{empered}} = \, \begin{matrix} \langle \, 2^{\, \frac{1}{12}} \, { \rangle }_{T_{empered}} \, \end{matrix} \, [ \, f_{requency}(m_{ajor}s_{econd}) \, ]_{T_{empered}} = \, [ \, f_{requency}(d_o \, r_e) \, ]_{T_{empered}} \, = \, \begin{matrix} \langle \, 2^{\, \frac{2}{12}} { \rangle }_{T_{empered}} \, \end{matrix} \, [ \, f_{requency}(m_{inor}t_{hird}) \, ]_{T_{empered}} = \, [ \, f_{requency}(d_o \, {r_e}^{\#}) \, ]_{T_{empered}} \, = \, \begin{matrix} \langle \, 2^{\, \frac{3}{12}} { \rangle }_{T_{empered}} \, \end{matrix} \, [ \, f_{requency}(m_{ajor}t_{hird}) \, ]_{T_{empered}} = \, [ \, f_{requency}(d_o \, m_i) \, ]_{T_{empered}} \, = \, \begin{matrix} \langle \, 2^{\, \frac{4}{12}} { \rangle }_{T_{empered}} \, \end{matrix} \, [ \, f_{requency}(f_{ourth}) \, ]_{T_{empered}} = \, [ \, f_{requency}(d_o \, f_a) \, ]_{T_{empered}} \, = \, \begin{matrix} \langle \, 2^{\, \frac{5}{12}} { \rangle }_{T_{empered}} \, \end{matrix} \, [ \, f_{requency}(f_{ifth}) \, ]_{T_{empered}} = \, [ \, f_{requency}(d_o \, s_o) \, ]_{T_{empered}} \, = \, \begin{matrix} \langle \, 2^{\, \frac{7}{12}} { \rangle }_{T_{empered}} \, \end{matrix} \, [ \, f_{requency}(o_{ctave}) \, ]_{T_{empered}} = \, [ \, f_{requency}(d_o \, 2 d_o) \, ]_{T_{empered}} \, = \, \begin{matrix} \langle \, 2^{\, \frac{12}{12}} { \rangle }_{T_{empered}} \, \end{matrix} \,///////
Frequencies for diatonic intervals with pythagorean and equally tempered tuning:
\, \begin{matrix} \, I_{nterval} & S_{olfege} & P_{ythagorean}F_{requency} & T_{empered}F_{requency} \\ & & & & & & & \\ p_{rim} & d_o \, d_o & \frac{1}{1} & 2^{\, \frac{0}{12}} \\ m_{inor}s_{econd} & \;\; d_o \, {d_o}^{\#} & \frac{16}{15} & 2^{\, \frac{1}{12}} \\ m_{ajor}s_{econd} & d_o \, r_e & \frac{9}{8} & 2^{\, \frac{2}{12}} \\ m_{inor}t_{hird} & \;\,\, d_o \, {r_e}^{\#} & \frac{6}{5} & 2^{\, \frac{3}{12}} \\ m_{ajor}t_{hird} & \; d_o \, m_i & \frac{5}{4} & 2^{\, \frac{4}{12}} \\ f_{ourth} & d_o \, f_a & \frac{4}{3} & 2^{\, \frac{5}{12}} \\ & \;\,\, d_o \, {f_a}^{\#} & & 2^{\, \frac{6}{12}} \\ f_{ifth} & d_o \, s_o & \frac{3}{2} & 2^{\, \frac{7}{12}} \\ & \;\,\, d_o \, {s_o}^{\#} & & 2^{\, \frac{8}{12}} \\ s_{ixth} & d_o \, l_a & \frac{5}{3} & 2^{\, \frac{9}{12}} \\ s_{eventh} & \; d_o \, {t_i}_b & \frac{16}{9} & 2^{\, \frac{10}{12}} \\ m_{ajor}s_{eventh} & d_o \, t_i & \frac{15}{8} & 2^{\, \frac{11}{12}} \\ o_{ctave} & \;\;\, d_o \, 2 d_o & \frac{2}{1} & \, 2^{\, \frac{12}{12}} \, \end{matrix} \,///////
Simulate “the tempered whistler”
///////
• Minor
Table of intervals in music theory
Intervals:
• prim
• second
• minor second
• major second
• third
• minor third
• major third
• perfect fourth
• tritone = augmented fourth = diminished fifth
• perfect fifth
• augmented fifth
• major sixth
• minor seventh
• major seventh
• perfect octave





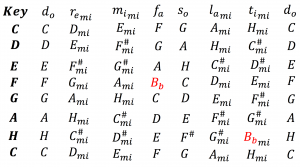



You are a very clever individual!