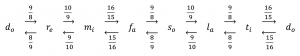This page is a sub-page of our page on Music.
///////
Related KMR-pages:
///////
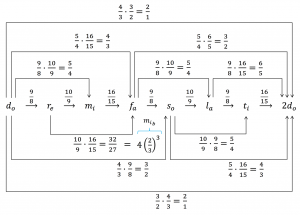
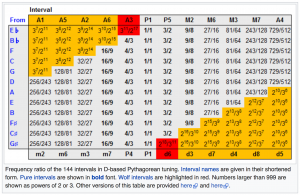
The basic pythagorean tuning intervals:
G♯♭
A comparison between pythagorean and tempered piano tuning
\, \begin{matrix} \\ -6 & G^{\text{♭}} & \left(\ 3/2 \right)^{-6} = 2^{-4} \times 2^{10}/3^6 & 2^{10}/3^6 & - & 2^{\, 6/12} & ≈ & - 0.0095 & \text{♭ ♭ ♭ ♭ ♭ ♭} \\ -5 & C^{\text{♯}} & \left( 3/2 \right)^{-5} = 2^{-3} \times 2^8/3^5 & 2^8/3^5 & - & 2^{\, 1/12} & ≈ & -0.0060 & \text{♭ ♭ ♭ ♭ ♭} \\ -4 & G^{\text{♯}} & \left( 3/2 \right)^{-4} = 2^{-3} \times 2^7/3^4 & 2^7/3^4 & - & 2^{\, 8/12} & ≈ & -0.0072 & \text{♭ ♭ ♭ ♭} \\ -3 & D^{\text{♯}} & \left( 3/2 \right)^{-3} = 2^{-2} \times 2^5/3^3 & 2^5/3^3 & - & 2^{\, 3/12} & ≈ & -0.0040 & \text{♭ ♭ ♭} \\ -2 & B^{\text{♭}} & \left( 3/2 \right)^{-2} = 2^{-2} \times 2^4/3^2 & 2^4/3^2 & - & 2^{\, 10/12} & ≈ & -0.0040 & \text{♭ ♭} \\ -1 & F & \left( 3/2 \right)^{-1} = 2^{-1} \times 2^2/3^1 & 2^2/3^1 & - & 2^{\, 5/12} & ≈ & -0.0015 & \text{♭} \\ \; 0 & C & \left( 3/2 \right)^{\, 0} = 2^{\, 0} \times 3^{\, 0}/2^{\, 0} & 3^{\, 0}/2^{\, 0} & - & 2^{\, 0/12} & = & 0 & \\ \; 1 & G & \left( 3/2 \right)^1 = 2^{\, 0} \times 3^1/2^1 & 3^1/2^1 & - & 2^{\, 7/12} & ≈ & 0.0017 & \text{♯} \\ \; 2 & D & \left( 3/2 \right)^2 = 2^1 \times 3^2/2^3 \, & 3^2/2^3 & - & 2^{\, 2/12} & ≈ & 0.0025 & \text{♯ ♯} \\ \; 3 & A & \left( 3/2 \right)^3 = 2^1 \times 3^3/2^4 \, & 3^3/2^4 & - & 2^{\, 9/12} & ≈ & 0.0057 & \text{♯ ♯ ♯} \\ \; 4 & E & \left( 3/2 \right)^4 = 2^2 \times 3^4/2^6 \; & 3^4/2^6 & - & 2^{\, 4/12} & ≈ & 0.0057 & \text{♯ ♯ ♯ ♯} \\ \; 5 & B & \left( 3/2 \right)^5 = 2^2 \times 3^5/2^7 \; & 3^5/2^7 & - & 2^{\, 11/12} & ≈ & 0.0107 & \text{♯ ♯ ♯ ♯ ♯} \\ \; 6 & F^{\text{♯}} & \left(\ 3/2 \right)^6 = 2^3 \times 3^6/2^9 \;\, & 3^6/2^9 & - & 2^{\, 6/12} & ≈ & 0.0096 & \text{♯ ♯ ♯ ♯ ♯ ♯} \\ \; 7 & C^{\text{♯}} & \left( 3/2 \right)^7 = 2^4 \times 3^7/2^{11} & 3^7/2^{11} & - & 2^{\, 1/12} & ≈ & 0.0084 & \text{♭ ♭ ♭ ♭ ♭} \\ \; 8 & G^{\text{♯}} & \left( 3/2 \right)^8 = 2^4 \times 3^8/2^{12} & 3^8/2^{12} & - & 2^{\, 8/12} & ≈ & 0.0144 & \text{♭ ♭ ♭ ♭} \\ \; 9 & D^{\text{♯}} & \left( 3/2 \right)^9 = 2^5 \times 3^9/2^{14} & 3^9/2^{14} & - & 2^{\, 3/12} & ≈ & 0.0121 & \text{♭ ♭ ♭} \\ 10 & B^{\text{♭}} & \left( 3/2 \right)^{10} = 2^5 \times 3^{10}/2^{15} & 3^{10}/2^{15} & - & 2^{\, 10/12} & ≈ & 0.0202 & \text{♭ ♭} \\ 11 & F & \left( 3/2 \right)^{11} = 2^6 \times 3^{11}/2^{17} & 3^{11}/2^{17} & - & 2^{\, 5/12} & ≈ & 0.0167 & \text{♭} \\ 12 & C & \left( 3/2 \right)^{12} = 2^7 \times 3^{12}/2^{19} & 3^{12}/2^{19} & - & 2^{\, 12/12} & ≈ & 0.0136 & \end{matrix} \,
///////
\, \begin{matrix} \\ 0 & C & 1 = \left( 3/2 \right)^0 = 3^0/2^0 & 3^0/2^0 & - & 2^{\, 0/12} & = & 0 & \text{0 ♯} \\ 1 & G & \left( 3/2 \right)^1 = 3^1/2^1 & 3^1/2^1 & - & 2^{\, 7/12} & ≈ & 0.0017 & \text{♯} \\ 2 & D & \left( 3/2 \right)^2 = 2^1 \times 3^2/2^3 \, & 3^2/2^3 & - & 2^{\, 2/12} & ≈ & 0.0025 & \text{♯ ♯} \\ 3 & A & \left( 3/2 \right)^3 = 2^1 \times 3^3/2^4 \, & 3^3/2^4 & - & 2^{\, 9/12} & ≈ & 0.0057 & \text{♯ ♯ ♯} \\ 4 & E & \left( 3/2 \right)^4 = 2^2 \times 3^4/2^6 \; & 3^4/2^6 & - & 2^{\, 4/12} & ≈ & 0.0057 & \text{♯ ♯ ♯ ♯} \\ 5 & B & \left( 3/2 \right)^5 = 2^2 \times 3^5/2^7 \; & 3^5/2^7 & - & 2^{\, 11/12} & ≈ & 0.0107 & \text{♯ ♯ ♯ ♯ ♯} \\ 6 & F^{\text{♯}} & \left(\ 3/2 \right)^6 = 2^3 \times 3^6/2^9 \;\, & 3^6/2^9 & - & 2^{\, 6/12} & ≈ & 0.0096 & \text{♯ ♯ ♯ ♯ ♯ ♯ = ♭ ♭ ♭ ♭ ♭ ♭} \\ 7 & C^{\text{♯}} & \left( 3/2 \right)^7 = 2^4 \times 3^7/2^{11} & 3^7/2^{11} & - & 2^{\, 1/12} & ≈ & 0.0084 & \text{♭ ♭ ♭ ♭ ♭} \\ 8 & G^{\text{♯}} & \left( 3/2 \right)^8 = 2^4 \times 3^8/2^{12} & 3^8/2^{12} & - & 2^{\, 8/12} & ≈ & 0.0144 & \text{♭ ♭ ♭ ♭} \\ 9 & D^{\text{♯}} & \left( 3/2 \right)^9 = 2^5 \times 3^9/2^{14} & 3^9/2^{14} & - & 2^{\, 3/12} & ≈ & 0.0121 & \text{♭ ♭ ♭} \\ 10 & B^{\text{♭}} & \left( 3/2 \right)^{10} = 2^5 \times 3^{10}/2^{15} & 3^{10}/2^{15} & - & 2^{\, 10/12} & ≈ & 0.0202 & \text{♭ ♭} \\ 11 & F & \left( 3/2 \right)^{11} = 2^6 \times 3^{11}/2^{17} & 3^{11}/2^{17} & - & 2^{\, 5/12} & ≈ & 0.0167 & \text{♭} \\ 12 & C & \left( 3/2 \right)^{12} = 2^7 \times 3^{12}/2^{19} & 3^{12}/2^{19} & - & 2^{\, 12/12} & ≈ & 0.0136 & \text{0 ♭ = 0 ♯} \end{matrix} \,///////
According to legend, the pythagoreans used to explore the structure of numbers by arranging pebbles in regular patterns that became known as “figures”. In the rectangular pattern below they discovered the basic pythagorean tuning intervals:
\, \begin{matrix} & & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ & & & & & & & & & & & & & & & & & & & & & & & & & & & & & & & & \\ 1 & & \blacksquare & 2/1 & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \square & \square & \blacksquare & \blacksquare & \square & \square & \square & \square & \square & \blacksquare \\ 2 & & \blacksquare & \blacksquare & 3/2 & \blacksquare & \blacksquare & \blacksquare & \square & \square & \blacksquare & \blacksquare & \square & \square & \square & \square & \square & \blacksquare \\ 3 & & \blacksquare & \blacksquare & \blacksquare & 4/3 & \blacksquare & \blacksquare & \square & \square & \blacksquare & \blacksquare & \square & \square & \square & \square & \square & \blacksquare \\ 4 & & \blacksquare & \blacksquare & \blacksquare & \blacksquare & 5/4 & \blacksquare & \square & \square & \blacksquare & \blacksquare & \square & \square & \square & \square & \square & \blacksquare \\ 5 & & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & 6/5 & \square & \square & \blacksquare & \blacksquare & \square & \square & \square & \square & \square & \blacksquare \\ 6 & & \square & \square & \square & \square & \square & \square & \square & \square & \blacksquare & \blacksquare & \square & \square & \square & \square & \square & \blacksquare \\ 7 & & \square & \square & \square & \square & \square & \square & \square & \square & \blacksquare & \blacksquare & \square & \square & \square & \square & \square & \blacksquare \\ 8 & & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & 9/8 & \blacksquare & \square & \square & \square & \square & \square & \blacksquare \\ 9 & & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & 10/9 & \square & \square & \square & \square & \square & \blacksquare \\ 10 & & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \blacksquare \\ 11 & & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \blacksquare \\ 12 & & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \blacksquare \\ 13 & & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \blacksquare \\ 14 & & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \square & \blacksquare \\ 15 & & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & \blacksquare & 16/15 \end{matrix} \,///////
From Wikipedia:
/////// OBS: The magic triangles described below are NOT related to pythagorean intervals.
Magic triangle:
\; \;\; 1 \; = \; 1 \; = \; 1 \, \times \, 1 \, \times \, 1 \;
\;\;\; 3 \; + \;\; 5 \; = \; 8 \; = \; 2 \, \times \, 2 \, \times \, 2 \;
\;\;\; 7 \; + \;\; 9 \;\, + \, 11 \; = \; 27 \; = \; 3 \, \times \, 3 \, \times \, 3 \;
\; 13 \; + \; 15 \; + \, 17 \; + \; 19 \; = \; 64 \; = \; 4 \, \times \, 4 \, \times \, 4 \;
\; 21 \; + \; 23 \; + \, 25 \; + \; 27 \; + \; 29 \; = \; 125 \; = \; 5 \, \times \, 5 \, \times \, 5 \;
\; 31 \; + \; 33 \; + \, 35 \; + \; 37 \; + \; 39 \; + 41 \; = \; 216 \; = \; 6 \, \times \, 6 \, \times \, 6 \;
\; \cdots \;
Moreover, we have:
\; 1 \; = \; 1^2 \;
\; 1 \; + \; 3 \; = 4 \; = \; 2^2 \;
\; 1 \; + \; 3 \; + \; 5 \; = 9 \; = \; 3^2 \;
\; 1 \; + \; 3 \; + \; 5 \; + \; 7 \; = 16 \; = \; 4^2 \;
\; 1 \; + \; 3 \; + \; 5 \; + \; 7 \; + \; 9 \; = 25 \; = \; 5^2 \;
\; 1 \; + \; 3 \; + \; 5 \; + \; 7 \; + \; 9 \; + \; 11 \; = 36 \; = \; 6^2 \;
\; \cdots \;
Both these triangles can be continued indefinitely.
///////