This page is a sub-page of our page on Music.
///////
Related KMR-pages:
• Shift of Basis (in general).
///////
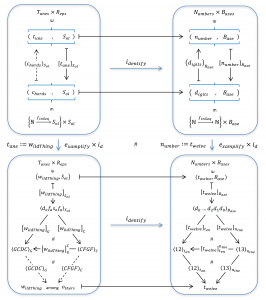
Representation and Reconstruction of a Presentant with respect to a Background
Representation: \, [ \, p_{resentant} \, ]_{B_{ackground}} \, \mapsto \, \left< \, r_{epresentant} \, \right>_{B_{ackground}}
Reconstruction: \, \left( \, \left< \, r_{epresentant} \, \right>_{B_{ackground}} \, \right)_{B_{ackground}} \mapsto \,\, p_{resentant}
/////// In Swedish:
Representation och Rekonstruktion av en Presentant med avseende på en Bakgrund
Representation: \, [ \, p_{resentant} \, ]_{B_{akgrund}} \, \mapsto \, \left< \, r_{epresentant} \, \right>_{B_{akgrund}}
Rekonstruktion: \, \left( \, \left< \, r_{epresentant} \, \right>_{B_{akgrund}} \, \right)_{B_{akgrund}} \mapsto \,\, p_{resentant}
/////// Back to English:
Representation and Reconstruction of a \, t_{une} \, with respect to an \, A_{rrangement} \, :
Representation: [ \, t_{une} \, ]_{A_{rr}} = \left< \,s_{core} \, \right>_{A_{rr}} .
Reconstruction: \left(\left< \, s_{core} \, \right>_{A_{rr}}\right)_{A_{rr}} = t_{une} .
s_{core} \, is another name for Sheet music. Here we will model it as:
s_{core} = \{ \, o_{rchestration}, c_{horeography} \, \}
where \, o_{rchestration} \, specifies which instruments that are involved in the \, A_{rrangement} \, , and \, c_{horeography} \, specifies how these instruments should interact with each other.
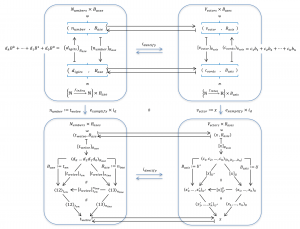
Representation and Reconstruction of Numbers and Tunes
The Representation and Reconstruction formulas for Numbers carry over to corresponding partial representation and partial reconstruction formulas for Tunes.
In tonal music, the tonal \, B_{ase} \, , the so-called tonic, of a \, t_{une} \, is given by its \, K_{ey} \, .
In the case of numbers and their digits with respect to a base, knowledge of the digits and the base is enough to uniquely determine the underlying number.
In contrast, in the case of tunes and their chord-sequences with respect to a key, knowledge of the chord-sequence and the key is NOT enough to uniquely determine the underlying tune. There are a lots of other aspects of a tune (such as melody, rhythm, etc) that are part of its arrangement.
Hence, while a \, n_{umber} \, is totally represented by its \, d_{igits} \, with respect to a certain \, B_{ase} \, , a \, t_{une} \, is only partially represented by its \, c_{hordSequence} \, with respect to a certain \, K_{ey} \,.
Therefore, in the case of tunes and their chord-sequences with respect to different keys, we can only state that:
Partial Representation: [ \, t_{une} \, ]_{A_{rr}} \supset [ \, t_{une} \, ]_{K_{ey}} = \left< \,c_{hordSequence} \, \right>_{K_{ey}} \, .
Partial Reconstruction: {\left( \left< \, c_{hordSequence} \, \right>_{K_{ey}} \, \right)}_{K_{ey}} \supset t_{une} \, .
///////
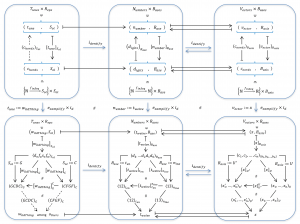
The Partial Base-Shift formula for Tunes
The Base-Shift formula for Numbers carries over to a Partial Base-Shift formula for Tunes. So does the Basis-Shift formula for Vectors.
It will be useful to have a symbolic name for the operation of shifting the \, K_{ey} \, of a \, t_{une} \, from \, {K_{ey}}_1 \, to \, {K_{ey}}_2 \,. This operation will be called \, K_{eyShift} \, and its action on a given \, t_{une} \, will be expressed in three different ways:
i) \, {[K_{eyShift}]}_{{K_{ey}}_2}^{{K_{ey}}_1} \, or
ii) \, {[t_{une}]}_{{K_{ey}}_2}^{{K_{ey}}_1} \, if the \, K_{eyShift} \, operation is clear from the context, or
iii) \, {[\,\,\,]}_{{K_{ey}}_2}^{{K_{ey}}_1} \, if both the \, t_{une} \, and the \, K_{eyShift} \, operation are clear from the context.
///////
{[t_{une}]}_{{K_{ey}}_2} \equiv {[K_{eyShift}]}_{{K_{ey}}_2}^{{K_{ey}}_1} {[t_{une}]}_{{K_{ey}}_1} \equiv {[t_{une}]}_{{K_{ey}}_2}^{{K_{ey}}_1} {[t_{une}]}_{{K_{ey}}_1} \, .
{[w_{ildThing}]}_G \equiv {[K_{eyShift}]}_G^C {[w_{ildThing}]}_C \equiv {[w_{ildThing}]}_G^C {[w_{ildThing}]}_C \, .
{[w_{ildThing}]}_C \equiv \left< \, CFGF \, \right>_C \equiv {\begin{bmatrix} d_o & f_a & s_o & f_a \\ \downarrow & \downarrow & \downarrow & \downarrow \\ C & F & G & F \end{bmatrix}}_C^{S_{ol}} \left< \, d_o f_a s_o f_a \, \right>_{S_{ol}} \,
{[w_{ildThing}]}_G \equiv \left< \, GCDC \, \right>_G \equiv {\begin{bmatrix} C & F & G & F \\ \downarrow & \downarrow & \downarrow & \downarrow \\ G & C & D & C \end{bmatrix}}_G^C \left< \, CFGF \, \right>_C \,
///////
Numbers are naturally related to Music:
///////
Numbers and Vectors are naturally related to each other:
Hence Numbers and Vectors are naturally equivalent.
Numbers and Vectors are naturally related to Music:
///////
Check out our section on Category Theory
///////