Representation and Reconstruction | Knowledge Management Research Group

This page is a sub-page of our page on Numbers.

///////

Representation and Reconstruction of a Number with respect to a Base

Representation: $[ \, n_{umber} \, ]_{B_{ase}} = \left< \, d_{igits} \, \right>_{B_{ase}}$

Reconstruction: $\left( \, \left< \, d_{igits} \, \right>_{B_{ase}} \, \right)_{B_{ase}} = n_{umber}$

////////// In Swedish:

Representation och Rekonstruktion av ett Tal med avseende på en Bas

Representation: $[ \,t_{al} \, ]_{B_{as}} = \left< \, s_{iffror} \, \right>_{B_{as}}$

Rekonstruktion: $\left( \, \left< \, s_{iffror} \, \right>_{B_{as}} \, \right)_{B_{as}} = t_{al}$

///////

The Hindu-Arabic Position System:

Choose a fixed $n_{umber}$ and call it the $B_{ase}$ . The $d_{igits}$ of any $n_{umber}$ with respect to this $B_{ase}$ are given by the sequence $\left<d_k ... d_2 d_1 d_0 \right>$ where $k + 1$ is the number of digits of the $n_{umber}$ with respect to this $B_{ase}$ . Hence we have:

$[n_{umber}]_{B_{ase}} \equiv \left<d_{igits}\right>_{B_{ase}} \equiv \left< d_k ... d_2 d_1 d_0 \right>_{B_{ase}} \,$ , and

$n_{umber} \equiv \left(\left< d_k ... d_2 d_1 d_0 \right>_{B_{ase}}\right)_{B_{ase}} \equiv d_k B_{ase}^{\,k} + ... + d_2 B_{ase}^{\,2} + d_1 B_{ase}^{\,1} + d_0 B_{ase}^{\,0} \, .$

In order to shorten this expression, let us denote the chosen $B_{ase}$ by $B$ .

Since $B^1 \equiv B$ and $B^0 \equiv 1 \,$ , we can write:

$n_{umber} \equiv d_k B^k + ... + d_2 B^2 + d_1 B^1 + d_0 B^0 \equiv d_k B^k + ... + d_2 B^2 + d_1 B + d_0 \, .$

////////////////////////////////////////

Experiment here
with trying to anticipate the $\, d_{igits} \,$
of a selected $\, n_{umber} \,$
relative to a selected $\, B_{ase} \,$ .

////////////////////////////////////////

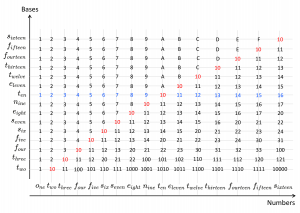
Representations of numbers in different bases:

Digits for numbers in different bases:

The numbers a and b represented in the bases x and y :

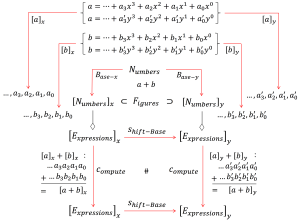
Let us choose the number $x$ as the $B_{ase}$ . For any numbers $\, a \,$ and $\, b \,$ we then have

$a \equiv {\left([\, a \, ]_x \right)}_x \equiv \cdots + a_3 x^3 + a_2 x^2 + a_1 x^1 + a_0 x^0$ , and

$b \equiv {\left([\, b \, ]_x \right)}_x \equiv \, \cdots + \, b_3 x^3 + b_2 x^2 + b_1 x^1 + b_0 x^0 \,$ , and we get:

$a+b \equiv \cdots + (a_3 + b_3) x^3 + (a_2 + b_2) x^2 + (a_1 + b_1) x^1 + (a_0 + b_0) x^0$ .

Therefore we have:

$[a + b]_x \equiv [a]_x + [b]_x$ ,

and hence:

$a + b \equiv \left([a]_x \right)_x + \left([b]_x \right)_x \equiv \left([a]_x + [b]_x \right)_x \equiv \left([a + b]_x \right)_x \,$ , as it should be.

If we choose the number $\, y \,$ as the $\, B_{ase} \,$ we have analogously:

$a \equiv {\left([\, a \, ]_y \right)}_y \equiv \, \cdots + a'_3 y^3 + a'_2 y^2 + a'_1 y^1 + a'_0 y^0$ .

$b \equiv {\left([\, b \, ]_y \right)}_y \equiv \, \cdots + \, b'_3 y^3 + b'_2 y^2 + b'_1 y^1 + b'_0 y^0$ .

//////////// TO BE CONTINUED SO THAT THE ENTIRE DIAGRAM ABOVE IS EXPLAINED.

The numbers twelve and eleven in the bases ten and three:

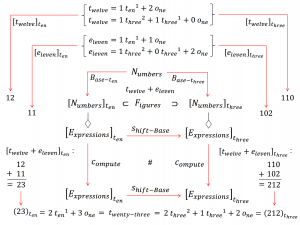
Since $\, t_{welve} \equiv 1 \, {t_{en}}^1 + 2 \, o_{ne} \,$ , we have

$[t_{welve}]_{t_{en}} = \left< 12 \right>_{t_{en}} \$ , and since

$t_{welve} \equiv 1 \, {t_{hree}}^2 + 1 \, {t_{hree}}^1 + 0 \, o_{ne} \,$ , we have

$[t_{welve}]_{t_{hree}} = \left< 110 \right>_{t_{hree}}$ .

In the same way we have:

$\, e_{leven} \equiv 1 \, {t_{en}}^1 + 1 \, o_{ne} \,$ , and thus $[e_{leven}]_{t_{en}} = \left< 11 \right>_{t_{en}} \,$ , as well as

$\, e_{leven} \equiv 1 \, {t_{hree}}^2 + 0 \, {t_{hree}}^1 + 2 \, o_{ne} \,$ , and thus $\, [e_{leven}]_{t_{hree}} = \left< 102 \right>_{t_{hree}}$ .

From the observations above, we can compute

$[t_{welve} + e_{leven}]_{t_{en}} \equiv \left<\, 12 \; + \, 11 \, \right>_{t_{en}} \equiv \left<\, 23 \, \right>_{t_{en}}\;$ , and

$[t_{welve} + e_{leven}]_{t_{hree}} \equiv \left<\, 110 \; + \, 102 \,\right>_{t_{hree}} \equiv \left<\, 212 \,\right>_{t_{hree}} \;$ .

Now, since:

$2 \, {t_{en}}^1 + 3 \, o_{ne} \equiv 2 \, {t_{hree}}^2 + 1 \, {t_{hree}}^1 + 2 \, o_{ne} \equiv t_{wentyThree} \;$ , we have

$\left(\left<\, 23 \,\right>_{t_{en}}\right)_{t_{en}} \equiv \left(\left< \, 212 \, \right>_{t_{hree}}\right)_{t_{hree}} \equiv t_{wentyThree} \,$ .

Getting rid of the carry problem

Idea: When we want to compute a certain operation, say $\, a + b \times c$ , we can always choose a base that is big enough, so that carrying out the operation will involve no “carry problems”, i.e., no “overflow” of digits within any power of the base. In fact, for any given finite sequence of binary operations/computations, there is a smallest natural number $\, B$ , such that the choice of $\, B \,$ as a basis for the computation involves no carrying of any digits across different powers of $\, B$ .

Hence, with this definition, each computation involving ‘plus’ and ‘times’ induces a ring homomorphism on the polynomial ring presented by the symbols of the operation/computation, i.e., the Base chosen for it and the digits involved in it.

///////

$\, o_{ne} \, t_{wo} \, t_{hree} \, f_{our} \, f_{ive} \, s_{ix} \, s_{even} \, e_{ight} \, n_{ine} \, t_{en} \,$
$\, e_{leven} \, t_{welve} \, t_{hirteen} \, f_{ourteen} \, f_{ifteen} \, s_{ixteen} \,$

///////

Representation: $[ \, aN_{umber} \, ]_B = \left< \, i_{ts}d_{igits} \, \right>_B$

Reconstruction: $\left( \, [ \, aN_{umber} \, ]_B \, \right)_B = t_{he}N_{umber}$

///////

$\, (m + m') \times (n + n') \, =$

$\, = \, \left( \, [ \, (m + m') \times (n + n') \, ]_B \, \right)_B \, =$

$\, = \, \left( \, [ \, (m + m') \, ]_B \times [ \, (n + n') \, ]_B \, \right)_B \, =$

$\, = \left( \, \left< \, ( \displaystyle\sum_{i=1}^{B-1} (m_i + m'_i) b^i) \times (\displaystyle\sum_{j=1}^{B-1} (n_j + n'_j) b^j) \, \right>_B \, \right)_B \, =$

$\, = \left( \, \left< \, ( \displaystyle\sum_{i=1}^{B-1} m_i b^i + \displaystyle\sum_{i=1}^{B-1} m'_i b^i) \times (\displaystyle\sum_{j=1}^{B-1} n_j b^j + \displaystyle\sum_{j=1}^{B-1} n'_j b^j) \, \right>_B \, \right)_B \, =$

$\, = \left( \, \left< \, \displaystyle\sum_{i+j=k}^{k=B-1} ( m_i b^i \times n_j b^j + m_i b^i \times n'_j b^j + m'_i b^i \times n_j b^j + m'_i b^i \times n'_j b^j ) \, \right>_B \, \right)_B \, =$

$\, = \left( \, \left< \, (\displaystyle\sum_{i+j=k}^{k=B-1} m_i n_j b^{i+j} + \displaystyle\sum_{i+j=k}^{k=B-1} m_i n'_j b^{i+j} + \displaystyle\sum_{i+j=k}^{k=B-1} m'_i n_j b^{i+j} + \displaystyle\sum_{i+j=k}^{k=B-1} m'_i n'_j b^{i+j} ) \, \right>_B \, \right)_B \, =$

$\, = \, \left( \, [ \, m n \, ]_B + [ \, m n' \, ]_B + [ \, m' n \, ]_B + [ \, m' n' \, ]_B \, \right)_B \, =$

$\, = \, \left( \, [ \, m n + m n' + m' n + m' n' \, ]_B \, \right)_B \, =$

$\, = \, m n + m n' + m' n + m' n'$ .

///////

Leave a Reply Cancel reply