This page is a sub-page of the page on our Learning Object Repository
///////
The sub-pages of this page are:
• Business Algebra
• Clifford Algebra
• Geometric Algebra
• Linear Algebra
• Matrix Algebra
• Knowledge Algebra
• Discourse Algebra
• Social Algebra
• Some basic algebraic concepts
///////
Related KMR-pages:
• Socially Responsible Algebra
• Norm-Critical Innovation Algebra
• Artificial Ethics
///////
Other relevant sources of information:
• Algebra
• Coalgebra
• Measuring coalgebra
• F-coalgebra
///////
Anchors into the text below
• ‘algebra’ versus ‘an algebra’
///////
Emmy Noether: The Newton of Algebra and the grandmother of Category Theory:
• Emmy Noether (at Wikipedia)
• Emmy Noether, BBC: In Our Time. Melvyn Bragg and guests discuss the ideas
of one of the great 20th-century mathematicians.
• Emmy Noether (at famousmathematicians.net)
• The origins of mathematical abstraction, by Saunders Mac Lane, 1999.
• Category theory
///////
Saunders Mac Lane and Samuel Eilenberg: The fathers of category theory
• Categories for the Working Mathematician, by Saunders Mac Lane, Springer Verlag, 1971.
/////// ‘algebra’ versus ‘an algebra’
‘algebra’_versus_’an algebra’
What is ‘algebra‘ and what is meant by ‘an algebra‘ ?
By the collective (= non-plurizable) term ‘algebra‘ one usually means the domain that studies all forms of different computational systems.
Definition: In this context the expression ‘an algebra‘ will refer to a computational system involving two operations where at least one of them distributes over the other.
REMARK: In a boolean algebra both operations have this property.
The operations of an algebra will are called ‘addition’ and ‘multiplication’ and denoted by ‘plus’ ( \, + \, ) respectively ‘times’ ( \, * \, ). The distributive relation between addition and multiplication can then be verbalized as “multiplication distributes over addition” and ‘formulized’ as
\,\,\,\,\,\,\, (a \, + \, b) * (c \, + \, d) \, = a * c \, + \, a * d \, + \, b * c \, + \, b * d \, .
NOTATION: If \, X \, is an algebra over the algebra \, Y \, under the conditions \, C \, ,
then one says that \, "X \, is a \, C -algebra over \, Y \, " .
Example 1:
The (commutative) algebra of polynomials in one variable with real coefficients.
A typical element of this algebra, a typical polynomial of one variable, can be expressed as
\, c_0 \, + \, c_1 x \, + \, c_2 x^2 \, + \, \cdots \, + \, c_n x^n ,
where \, x \, denotes the variable and \, {c_0, \, c_1, \, \cdots \, , c_n} \, denote the real coefficients.
Example 2: The clifford algebra \, C_l(e_1, e_2, e_3) \, in three variables \, e_1, e_2, e_3 \,
over the (algebra of) real numbers \, \mathbb{R} .
Let \, {\mathbb{E}}^3 \, denote the ordinary Euclidean 3-space with an orthonormal basis consisting of the vectors \, {e_1, e_2, e_3} . Orthogonality means that we have \, e_1 \perp e_2 \, , \, e_2 \perp e_3 \, , \, e_3 \perp e_1 \, and orthonormality means that we also have \, e_1 \cdot e_1 \, = \, e_2 \cdot e_2 \, = \, e_3 \cdot e_3 \, = 1 .
The exterior product \, a \wedge b \, of two vectors \, a \, and \, b \, in \, {\mathbb{E}}^3 \, represents an oriented, planar patch of surface, whose normal vector is parallel to the cross product \, a \times b \, and whose area is equal to the length of this vector. The orientation of the planar surface patch \, a \wedge b \, is seen in the anti-symmetry (= the sign-change) when we switch the order of \, a \, and \, b \, :
\, a \wedge b \, = \, - \, b \wedge a \, .
Geometrically this corresponds to changing the direction of the surface normal.
Let \, a \, and \, b \, be two non-zero vectors in \, {\mathbb{E}}^3 . From the properties of the cross product it follows that
\, a \wedge b = 0 \, if and only if \, a \, is parallel to \, b , a configuration that we denote by \, a \parallel b .
Given two vectors \, a \, , \, b \, \in {\mathbb{E}}^3 , William Kingdon Clifford defined their geometric product \, a \, b \, by
Definition: \, a \, b \, \stackrel {\mathrm{def}}{=} \, a \cdot b \, + \, a \wedge b .
We then have \, e_1 \, e_1 = e_1 \cdot e_1 + e_1 \wedge e_1 = 1 + 0 = 1 , and similar for \, e_2 \, and \, e_3 .
We can write these relationships as \; e_1^2 \, = \, e_2^2 \, = \, e_3^2 \, = \, 1 .
It is also evident from the definition of the geometric product that for two non-zero vectors \, a \, and \, b \, we have \, a \, b \, = \, a \wedge b \, if and only if \, a \perp b . Hence, for the orthonormal basis vectors \, e_i \in {\mathbb{E}}^3 , we have if \, i \neq j \, :
\, e_i \, e_j \, = \, e_i \wedge e_j \, = \, - \, e_j \wedge e_i \, = \, - \, e_j \, e_i .
///////
FACT: The non-commutative polynomial algebra \, {\mathbb{R}}\{e_1, e_2, e_3\} \, in three variables
with real coefficients is a clifford algebra over the real numbers \, \mathbb{R} .
NOTATION: This algebra is called \, C_l({\mathbb{E}}^3) or \, C_l(e_1, e_2, e_3) .
The Clifford conditions are given by
(1) \,\,\,\,\, e_1^2 = e_2^2 = e_3^2 = 1 , and
(2) \,\,\,\,\, e_k \, e_i = - \, e_i \, e_k \, if \, k \neq i .
From the associativity of the geometric product, and from its antisymmetry on the pairs of basis vectors \, e_1, e_2, e_3 , it follows that:
(3) \,\,\,\,\, (e_i e_k)^2 = e_i e_k e_i e_k = - e_k e_i e_i e_k = - e_k e_k = -1 \, if \, k \neq i , and that
(4) \,\,\,\,\, (e_1 e_2 e_3)^2 = e_1 e_2 e_3 e_1 e_2 e_3 = (-1)^2 e_1 e_1 e_2 e_3 e_2 e_3 = - e_2 e_2 e_3 e_3 = -1 .
Definitions:
1): The polynomials of vectors that appear in any clifford algebra
are called multivectors.
Example: The polynomial \, e_1 - 2 e_2 + \pi e_1 e_2 -3 e_2 e_3 + e_3 e_1 + e_1 e_2 e_3 \,
is a multivector in the clifford algebra \, C_l(e_1, e_2, e_3) . It has six terms.
2): The number of vectors that appear in each term of a multivector
is called the degree of the term.
Example: The degrees of the respective terms
of the polynomial \, e_1 - 2 e_2 + \pi e_1 e_2 -3 e_2 e_3 + e_3 e_1 + e_1 e_2 e_3 \,
are (from left to right): \, 1, 1, 2, 2, 2, 3 .
3): If each term of a multivector has the same degree
the multivector is called homogeneous.
Example: The multivector \, 2 e_1 e_2 -3 e_2 e_3 + e_3 e_1 \, is homogeneous with degree 2.
4): A multivector that can be written as an exterior product of \, k \, vectors
is called a \, k –blade or a blade of degree \, k .
Example: In the clifford algebra \, C_l(e_1, e_2, e_3) \, , \, e_1 e_2 \equiv e_1 \wedge e_2 \, is a \, 2 -blade
and \, e_1 e_2 e_3 \equiv e_1 \wedge e_2 \wedge e_3 \, is a \, 3 -blade.
5): The \, 3 -blade \, e_1 e_2 e_3 \, is called a unit pseudoscalar for \, C_l(e_1, e_2, e_3) .
///////
FACT 1: In any clifford algebra, the geometric product of any set of basis vectors
produces a pseudoscalar. Moreover, any two pseudoscalars for the algebra
differ only by a scalar factor.
FACT 2: A pseudoscalar dualizes every multivector that it operates on by multiplication.
///////
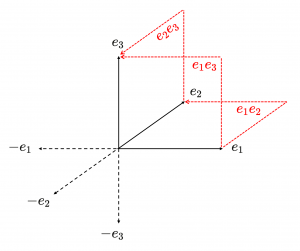
This diagram shows the 1-blades (unbroken black arrows) and the 2-blades (red, dotted, broken arrows) among the blades in the canonical basis for \, C_l(e_1, e_2, e_3) .
The negatives of the 1-blades are shown as dotted black arrows.
The 2-blades \, \textcolor {red} {e_1 e_2} \textcolor {black} {,} \textcolor {red} {e_2 e_3} \textcolor {black} {,} \textcolor {red} {e_1 e_3} \,
represent the directed area within the corresponding squares.
Example 3: The complex numbers represented as the even subalgebra
of the clifford algebra \, C_l(e_1, e_2) \, over the real numbers \, \mathbb{R} :
\, e_1, e_2 \,
\, e_1^2 = e_2^2 = 1 \,
\, e_2 e_1 = - e_1 e_2 \,
Hence we have: \, (e_1 e_2)^2 = e_1 e_2 e_1 e_2 = - e_2 e_1 e_1 e_2 = - e_2 e_2 = -1 –
\, \alpha_1 e_1 + \alpha_2 e_2 \,
\, \alpha'_1 e_1 + \alpha'_2 e_2 \,
\, (\alpha_1 e_1 + \alpha_2 e_2) (\alpha'_1 e_1 + \alpha'_2 e_2) =
\, = \alpha_1 e_1 \alpha'_1 e_1 + \alpha_1 e_1 \alpha'_2 e_2 + \alpha_2 e_2 \alpha'_1 e_1 + \alpha_2 e_2 \alpha'_2 e_2 \, =
= \, \alpha_1 \alpha'_1 e_1 e_1 + \alpha_2 \alpha'_2 e_2 e_2 + \alpha_1 \alpha'_2 e_1 e_2 + \alpha_2 \alpha'_1 e_2 e_1 \, =
= \, \alpha_1 \alpha'_1 + \alpha_2 \alpha'_2 + \alpha_1 \alpha'_2 e_1 e_2 - \alpha_2 \alpha'_1 e_1 e_2 \, =
= \, \alpha_1 \alpha'_1 + \alpha_2 \alpha'_2 + (\alpha_1 \alpha'_2 - \alpha_2 \alpha'_1) e_1 e_2 .
/////// The even part of the clifford algebra \, C_l(e_1, e_2) \, :
\, (x + y e_1 e_2) (x' + y' e_1 e_2) \, =
= \, x x' + x y' e_1 e_2 + y e_1 e_2 x' + y e_1 e_2 y' e_1 e_2 \, =
= \, x x' + x y' e_1 e_2 + y x' e_1 e_2 + y y' e_1 e_2 e_1 e_2 \, =
= \, x x' + x y' e_1 e_2 + y x' e_1 e_2 - y y' e_2 e_1 e_1 e_2 \, =
= \, x x' - y y' + (x y' + y x') e_1 e_2 .
///////