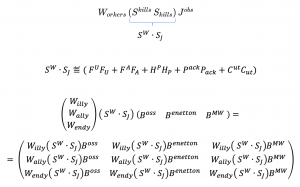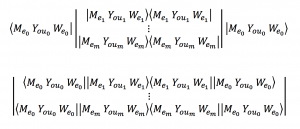This page is a sub-page of our page on Algebra.
///////
The sub-pages of this page are:
• The Universal Production Process
• Injecting Learning Loops
• User Modeling
• Experience Transfer
• Product Readiness
• The EE(S+O+C)(M+O+P) Model
• Corporate Training
• Bob’s Mail Order
• Innovation Hubs
• Ethical E-Commerce
////////
Related KMR-pages:
• Knowledge Algebra
• Discourse Algebra
• Social Algebra
• Social Calculus
• The Ericsson AXE10 Delay
• Disambiguating Equality
• Disambiguating Minus
• Disambiguating Plus
///////
Other related sources of information:
• TELLME D1.1 (v1.2).pdf State of the Art in Learning and Creativity Methodologies
in Manufacturing-related contexts.
• TELLME-D1.3-Annex(v2).docx Business Algebra:
A Mathematical Framework for Business Process Modeling.
• TELLME-D4.3-(v1 M18).pdf Integrated Industrial Workplace Model
Reference Implementation (Issue 1).
• TELLME-D4.4-(v2 M36).pdf Integrated Industrial Workplace Model
Reference Implementation Issue 2.
///////
Related EU/IST projects:
• TELL-ME (Technology Enhanced Learning LivingLabs for Manufacturing Environments)
• TEL-Map (Future gazing for Technology Enhanced Learning)
• ROLE (Responsive Open Learning Environments)
• PROLEARN (Network of Excellence on PROfessional LEARNing)
///////
Business Algebra (BA) is a business modeling application of Knowledge Algebra (KA) which is a matrix-based mathematical framework that enables dynamic overview of the model that you are developing (or executing) as well as combinatorial control over the options from which the successive choices are made.
Business Algebra makes use of knowledge algebra to capture and formalize a business model in terms of the terms that are used to talk about (i.e., to model) the business. These terms describe such things as processes, relations, goals, and conditions to name but a few. The parameters are obtained from how we talk about the business, the changes we want to realize are described by modeling the most important relationships among these parameters, and encapsulating some of these relationships into functions that help us to supply the corresponding parameters with values when calling the function with the corresponding arguments.
Describing a business in such terms is equivalent to building a model of the business based on these terms. As described in ch.35.1, parametrization of an area A subdivides it into entities and relationships that are specified by modeling the relationships between their corresponding parameters. The result is a model of A, as described in ch.35.2.
Anything that can be named and reasoned about can be modeled in knowledge algebra, including all chains of (possibly) relevant relations between all parameters that have been introduced in the model. Moreover, such relational chains can be evaluated both contextually and symbolically, allowing the symbols of a formal computation to change their relevance dynamically – by being connected to context-specific evaluations that bring in dynamic information from the outside. This feature of emerging relevance is at the heart of business algebra.
Moreover, through the use of feedback, knowledge algebra can support the construction of knowlecules that loop back on themselves. Such loops are well suited to model the ongoing shift in manufacturing, away from today’s traditional, linear, cause-effect oriented production models and towards more sustainable production models that are interacting with the emerging circular economy with its characteristic loops of systemic feedback.
Through their unique features, knowlecules provide the capacity necessary to represent arbitrarily-complex combinations of capabilities. This includes the capability to acquire new capabilities, which might arise through access to knowlecules created through some form of machine learning or self-regulated learning, or through a behaviourally-based form of training (whether socially-based such as Social Learning, or process-based such as Precision Teaching) or through a delegation mechanism such as Sub-contracting to an organization with the needed capability.
Arbitrary combinations of any of those options are feasible and the pros and cons of each combination can be modeled using business algebra. Also, business algebra can be used to model the potential capabilities that would arise by linking organisations, as in a Living Lab – or across a supply chain whose participants vary considerably in technology readiness level and in their ability to represent and to model their internal and external processes.
As a consequence, business algebra has the potential to accommodate double-loop organisational learning in high-complexity industrial systems as well as simpler (and normally more easily manageable) systems that are temporarily hard to control because some aspect of their environment (or their mode of use or their inherent technology or functionality) is undergoing evolutionary and/or radical change. In H2020, much attention is being paid to a major source of such changes: new KETs (key enabling technologies), ‘key’ in the sense of changing the landscape of production or maintenance (e.g., what is being made or maintained, how, by whom, where and with what cost). New KETs imply new know-how about how to use KETs in manufacturing, for example in knowledge-intensive tasks using new materials and new manufacturing processes. Some of that new know-how requires new threshold concepts, new mental models, new insights and new skills (e.g., in a work environment that includes autonomous ‘smart’ robots, a blue-collar worker will need to develop an appreciation of what kinds of training examples will be useful to those robots and how they will behave as a result of being exposed to those training examples).
///////
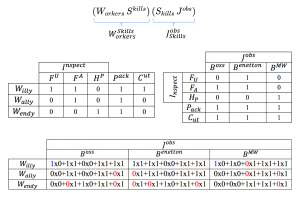
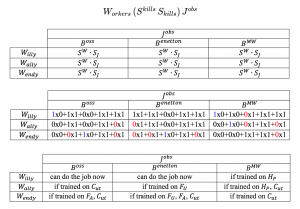
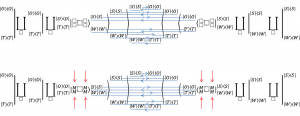
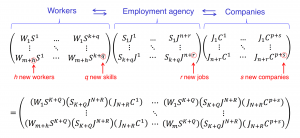
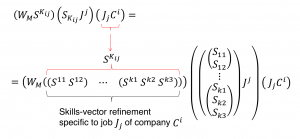
Matching of Workers and Jobs in terms of Skills:

///
\, \langle \, W_{orkers} \, \vert ( \vert \, S_{kills} \, \rangle \langle \, S_{kills} \, \vert ) \vert \, J_{obs} \, \rangle \, \equiv \, (\langle \, W_{orkers} \, \vert \vert \, S_{kills} \, \rangle ) ( \langle \, S_{kills} \, \vert \vert \, J_{obs} \, \rangle ) \, \equiv \, W_{orkers} \, ( S^{kills} \, S_{kills} ) \, J^{obs} \, \equiv \, ( W_{orkers} \, S^{kills} ) \, ( S_{kills} \, J^{obs} ) \,///////
/// EXPLAIN THE THREE COMPANIES JOB-SKILLS DEMANDS HERE
Willy, Wally, Wendy 1:
Willy, Wally, Wendy 2:
Willy, Wally, Wendy 3:
///////
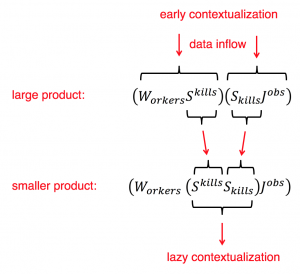
Early versus Lazy Contextualization:
///
///////
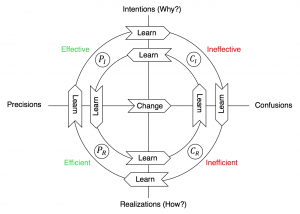
Change creates confusion – learning restores precision:
/////// The Universal Production Process:
Learning Injector Loops of the UPP:
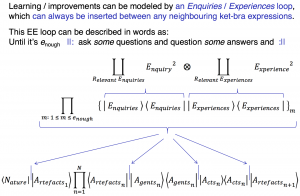
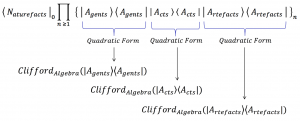
///////
Clifford Algebras of the UPP:
///////
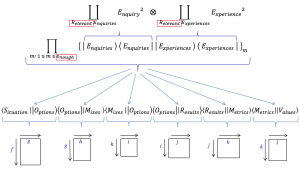
Mix and Match to Optimize:
///////
MMO – the emergence of relevance:
///////
Business Model Navigation:
///////
Experiences, Possibilities, Readiness, Action:
///////
Parametrizing over Business Models:
///////
Recursive Business Logic:
///////
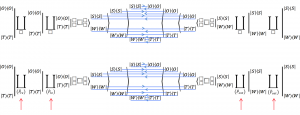
Dynamic Employment Agency
Dynamic employment agency 1:
Dynamic employment agency 2:
Dynamic employment agency 3:
Dynamic employment agency 4:
///////
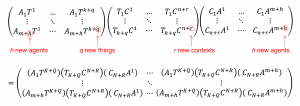
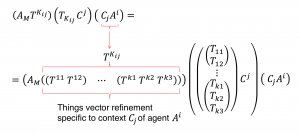
Connecting agents through things and contexts
Connecting agents through things and contexts 1:
Connecting agents through things and contexts 2:
Connecting agents through things and contexts 3:
///////
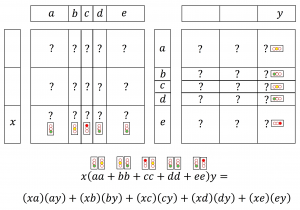
Dynamic evaluation of paths:
/////////////////
From me to you 1:
From me to you 2:
///////
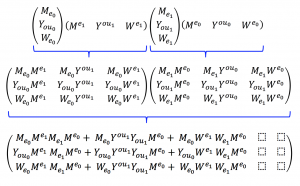
\, \langle \, a \, \vert \, \vert \, c \, \rangle \, = \, \langle \, a \, \vert \, \vert \, b \, \rangle \, \langle \, b \, \vert \, \vert \, c \, \rangle \, = \, \begin{pmatrix} a_1 b_1 & a_1 b_2 \\ a_2 b_1 & a_2 b_2 \end{pmatrix} \, \begin{pmatrix} b_1 c_1 & b_1 c_2 \\ b_2 c_1 & b_2 c_2 \end{pmatrix} \, = \, \begin{pmatrix} a_1 (b_1 b_1 + b_2 b_2) c_1 & a_1 (b_1 b_1 + b_2 b_2) c_2 \\ a_2 (b_1 b_1 + b_2 b_2) c_1 & a_2 (b_1 b_1 + b_2 b_2) c_2 \end{pmatrix} \,///////
\, \langle \, a \, \vert \, \vert \, b \, \rangle \, {\langle \, a \, \vert \, \vert \, b \, \rangle}^{\text{T}} = \langle \, a \, \vert \, \vert \, b \, \rangle \, \langle \, b \, \vert \, \vert \, a \, \rangle \, = \, \begin{pmatrix} a_1 b_1 & a_1 b_2 \\ a_2 b_1 & a_2 b_2 \end{pmatrix} \, \begin{pmatrix} b_1 a_1 & b_1 a_2 \\ b_2 a_1 & b_2 a_2 \end{pmatrix} \, = \, \begin{pmatrix} a_1 (b_1 b_1 + b_2 b_2) a_1 & a_1 (b_1 b_1 + b_2 b_2) a_2 \\ a_2 (b_1 b_1 + b_2 b_2) a_1 & a_2 (b_1 b_1 + b_2 b_2) a_2 \end{pmatrix} \,///////
\, \langle \, a \, \vert \, \vert \, b \, \rangle \, \langle \, b \, \vert \, \vert \, c \, \rangle \, \langle \, c \, \vert \, \vert \, d \, \rangle \, = \, \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \, \begin{pmatrix} b_1 & b_2 \end{pmatrix} \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} \, \begin{pmatrix} c_1 & c_2 \end{pmatrix} \, \begin{pmatrix} c_1 \\ c_2 \end{pmatrix} \, \begin{pmatrix} d_1 & d_2 \end{pmatrix} \, = \, = \, \begin{pmatrix} a_1 b_1 & a_1 b_2 \\ a_2 b_1 & a_2 b_2 \end{pmatrix} \, \begin{pmatrix} b_1 c_1 & b_1 c_2 \\ b_2 c_1 & b_2 c_2 \end{pmatrix} \, \begin{pmatrix} c_1 d_1 & c_1 d_2 \\ c_2 d_1 & c_2 d_2 \end{pmatrix} \, = \, \begin{pmatrix} a_1 (b_1 b_1 + b_2 b_2) (c_1 c_1 + c_2 c_2) d_1 & a_1 (b_1 b_1 + b_2 b_2) (c_1 c_1 + c_2 c_2) d_2 \\ a_2 (b_1 b_1 + b_2 b_2) (c_1 c_1 + c_2 c_2) d_1 & a_2 (b_1 b_1 + b_2 b_2) (c_1 c_1 + c_2 c_2) d_2 \end{pmatrix} \,///////