This page is a sub-page of our page on Business Algebra.
///////
The sub-pages of this page are:
• Replication (from a functorial perspective)
///////
What if a company could know (more of) what it actually knows? What if the implicit and largely unaware or highly localized knowledge that exists within a company could be made more explicit and available to all of its interested coworkers?
In this section we will address this issue – under the label of knowledge transfer within the company under consideration. We will also see how, by changing the name of a single index, we can change the resulting model to handling experience transfer between different companies. In fact, such inter-company experience transfer often happens informally, and goes by many names, such as e.g., “knowledge spill-overs”, “informal collaboration”, and “beer-to-beer learning”. According to Moretti (2012), knowledge spill-overs is one of three major interacting forces that together drive the rise and fall of innovation hubs.
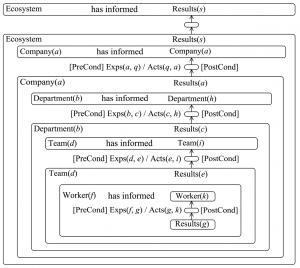
In classical matrix algebra, the value of any non-zero connectivity matrix element is 1, indicating that there is a connection between the corresponding elements, or, which amounts to the same thing, there is an edge between them in the graph that represents their connectivity. Such a matrix is called an adjacency matrix. A major innovation in Business Algebra is to allow the elements of an adjacency matrix to be “anything at all that is useful” in order to convey information about the connections that are focused on. Below we will be looking at formal multiplication of matrices of nested state diagrams, and we will show how this can convey complex and dynamic information on many different levels.
Knowledge transfer at the department level
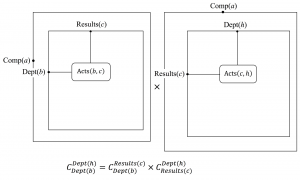
Let \, P_{Dept(b)}^{Results(c)} \, denote the progress state matrix for \, C_{ompany(a)} \, separated into the results of individual departments. The element \, (b, c) \, of this matrix denotes the state of progress of \, D_{epartment(b)} \, with respect to the set of \, R_{esults(c)} \, that it is aiming to achieve.
Moreover, let \, D_{Results(c)}^{Dept(h)} \, denote the dissemination state matrix of \, C_{ompany(a)} \, . This is a matrix whose element \, (c, h) \, contains the state of dissemination of the \, R_{esults(c)} \, achieved by \, D_{epartment(b)} \, with respect to transferring knowledge about these results to \, D_{epartment(h)} \, .
If we let \, K_{Dept(b)}^{Dept(h)} \, denote the knowledge transfer matrix from \, D_{epartment(b)} \, to \, D_{epartment(h)} \, , we can express this matrix as the product
\, K_{Dept(b)}^{Dept(h)} \triangleq P_{Dept(b)}^{Results(c)} \times D_{Results(c)}^{Dept(h)} \, .
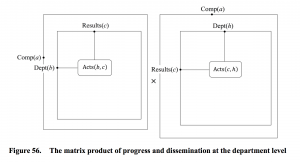
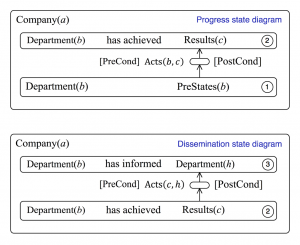
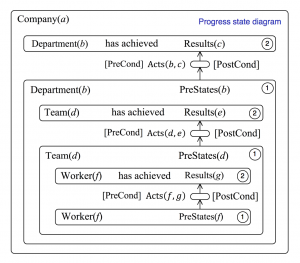
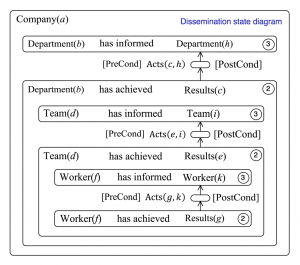
This model of knowledge transfer as a product of progress and dissemination is depicted in Figure 56. The element \, (b, h) \, of this matrix product consists of a sum over all the sets of \, R_{esults(c)} \, that \, D_{epartment(b)} \, is trying to achieve. As shown in Figure 56 and Figure 57, each term in this sum is itself a product of two state diagrams.
The progress state diagram (to the left) records the state of progress of \, D_{epartment(b)} \, with respect to achieving the \, R_{esults(c)} \, , and the dissemination state diagram (to the right) records the state of achievement of \, D_{epartment(b)} \, with respect to transferring knowledge about \, R_{esults(c)} \, to \, D_{epartment(h)} \, .
Figure 57 displays more detailed versions of the state diagrams that appear as matrix elements in Figure 56. The progress state diagram to the left of Figure 57 shows that, under the proper [PreConditions] the progress enters the “miniaturised state” in the middle. This state is in fact identical to the top-level state \, A_{cts}(b, c) \,, which appears in Figure 56. In this state of progress, the \, A_{cts}(b, c) \, of working towards the \, R_{esults(c)} \, are actually carried out. When the [PostConditions] are satisfied, the \, R_{esults(c)} \, have been achieved and progress enters the state “ \, D_{epartment(b)} \, has achieved \, R_{esults(c)} \, ”, which is labelled 2 in Figure 57.
Notice that state 2 is duplicated and appears both in the progress and the dissemination diagrams. Duplicating common states is a powerful way of connecting state diagrams that is complementary to message passing. Hence, as soon as \, R_{esults(c)} \, have been achieved, the state 2 at the bottom of the dissemination diagram is entered. Then \, D_{epartment(b)} \, starts establishing the [PreConditions] for dissemination of \, R_{esults(c)} \, to \, D_{epartment(h)} \, .
When these [PreConditions] have been established, the dissemination state transits to the small state in the middle, in which the \, A_{cts}(c, h) \, of dissemination towards \, D_{epartment(h)} \, are carried out. When (or if) the [PostConditions] for this state are fulfilled, the dissemination state changes into “ \, D_{epartment(b)} \, has informed \, D_{epartment(h)} \, ”, which is marked 3 in Figure 57, and the desired dissemination has been properly carried out.
To sum up, for each fixed value \, a \, (of some company reference index), the knowledge intra-transfer matrix of the corresponding \, C_{ompany(a)} \, can be written as the relational matrix product.
\, \left< \, D_{ept(b)} \, || \, D_{ept(h)} \, \right> \equiv \left< \, D_{ept(b)} \, || \, R_{esults(c)} \, \right> \left< \, R_{esults(c)} \, || \, D_{ept(h)} \, \right> \,or, in tensor notation:
\, K_b^h \equiv P_b^c \times D_c^h \, .
which is interpreted as
\, K_{Dept(b)}^{Dept(h)} \equiv P_{Dept(b)}^{Results(c)} \times D_{Results(c)}^{Dept(h)} \, ,
and which we recognize as the formula that was presented earlier.
//////////
CONTINUE HERE
//////////
Recursive tensor learning loops – confusions, enquiries, and experiences:
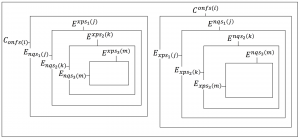
Experience Transfer:
Experience transfer within Company(a):
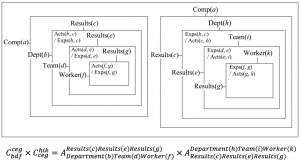
Experience transfer between Department(b) and Department(h) of Company(a) :
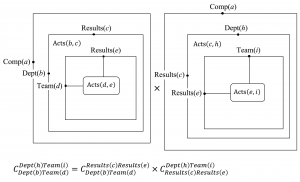
Experience transfer between Team(d) and Team(i) of Company(a):
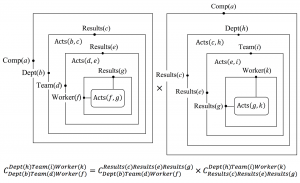
Experience transfer between Worker(f) and Worker(k) of Company(a):
Progress and Dissemination:
Progress and dissemination at the Department level of Company(a):
State of progress at the Team level of Company(a):

State of dissemination at the Team level of Company(a):

State of progress at the Worker level of Company(a):
State of dissemination at the Worker level of Company(a):
State of the effects on the Ecosystem of the activities of Company(a):
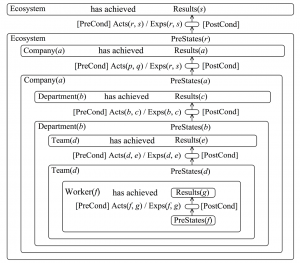
State of awareness about the effects on the Ecosystem
of the activities of Company(a):