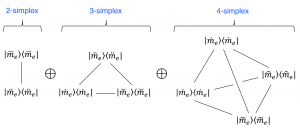
of an odd-party conversational simplex.
///////
This page is a sub-page of our page on Discourse Algebra.
///////
Related KMR pages:
• Combinatorial Clifford Algebra
• Knowledge Algebra
///////
Other related sources of information:
• Svensson & Naeve (2002): Combinatorial Aspects of Clifford Algebra.
///////
A conversational complex is a formal sum of conversational \, n -simplexes, where each \, n -simplex represents a conversation with \, n \, participants (also referred to as an \, n -party conversation.
Cohomology with respect to an odd-party conversational simplex:
NOTATION: Let \, P \, be a proposition, i.e., a logical statement which is either true or false.
Then \, (P) \, \stackrel {\mathrm{def}}{=} \, 1 \, if \, P \, is true, and \, (P) \, \stackrel {\mathrm{def}}{=} \, 0 \, if \, P \, is false.
Let \, C_l \, denote the Clifford algebra on \, n \, symbols \, e_1, e_2, ..., e_n \, over \, \mathbb{Z} \, and let \, C_l^- \, denote the subspace of odd multivectors of \, C_l . If we include the empty set \, \emptyset \, in the basis for \, C_l \, , then \, C_l \, has \, 2^n \, dimensions as a module over \, \mathbb{Z} .
For example, if \, n = 3 \, we have the \, 8 \, basis elements \, \emptyset \, , e_1 \, , e_2 \, , e_3 \, , e_1 e_2 \, , e_2 e_3 \, , e_3 e_1 \, , e_1 e_2 e_3 \, for the Clifford algebra \, C_l(e_1, e_2, e_3) .
On the basis elements of \, C_l \, the left inner product is defined as
\, X \, \llcorner \, Y \, \stackrel {\mathrm{def}}{=} \, (X \subseteq Y) X Y .
It is extended to all multivectors of \, C_l \, by linearity.
Here \, X Y \, denotes the geometric product of the multivectors \, X \, and \, Y in \, C_l .
On the basis elements of \, C_l \, the geometric product is defined as
\, A B \, \stackrel {\mathrm{def}}{=} \, \epsilon \, A \, \Delta \, B \, where \epsilon = \pm 1 and \, \Delta \, denotes symmetric difference.
The geometric product is extended to all multivectors of \, C_l \, by linearity.
On the basis elements of \, C_l \, the outer product is defined as
\, X \wedge \, Y \, \stackrel {\mathrm{def}}{=} \, ( X \cap Y = \emptyset ) X Y . It is extended to all multivectors of \, C_l \, by linearity.
Lemma 1: If \, X \in C_l^- \, then we have \, X \wedge X \, = \, 0 .
Proof: Exercise
Let \, S_n \, be an \, n -simplex in \, C_l \,
and let \, E = e_1 + e_2 + ... + e_n \, .
We define the boundary operator \, \partial \, by its action on each simplex \, S_n \,
of a complex of multivectors of \, C_l :
Definition: \, \partial S_n \, \stackrel {\mathrm{def}}{=} \, E \, \llcorner \, S_n .
=======
David Hestenes
=======
Making use of the following simple but important lemma
(whose proof is left as an exercise):
Lemma 2: \, A \, \llcorner \, (B \, \llcorner \, C) \, \equiv \, (A \wedge B) \, \, \llcorner \, \, C \,
we have
\, \partial \, ( \partial \, X ) \, = \, E \, \llcorner \, (E \, \llcorner \, X) \, = \, (E \wedge E) \, \llcorner \, X \, = \, 0 .
Since this holds for each multivector \, X \in C_l \, we can conclude that
\, \partial \, \circ \, \partial \, = \, 0 .
Moreover, \, \partial \, is a derivation and we have seen that \, {\partial}^2 = 0 . Therefore, for each odd simplex \, S_n , there is a cohomology on the corresponding odd-party conversational simplex.
///////