This page is a sub-page of our page on Discourse Algebra.
///////
1. Spacification of Discourses between Agents
Why would we want to “spacify discourses” that involve different (human and non-human) agents and create a discourse space? The reason is that such a space would provide a common background (= space) that is rich enough to include every single thread of discourse, i.e., everything that has ever been, is being, and will ever be expressed. Upon this background, any particular combination of discourse-threads can be positioned (= placed). Hence, as always, the reason for spacification is to explore different possibilities for placification.
2. Atomic and Aggregated Stories
The model that we will use to describe ”stories and other things” is depicted in Figure 4. In this model, Things are named entities that are experienced by humans either as phenomena that are part of the physical world that we perceive, or concepts that are part of the cognitive or mental world that we conceive. As described in Figure 4, stories are about things, but, at the same time, stories are (conceptual) things that belong to our mental world. This fact constitutes one of the challenges that confronts us when we are modeling stories.
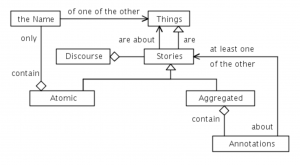
Figure 4: Atomic and Aggregated Stories
The model displays two kinds of stories: atomic stories and aggregated stories. Aggregated stories contain annotations about at least one of the other stories. Atomic stories contain only the name of one of the other things (i.e., some thing that is not a story). Hence, an atomic story can be regarded as a representative of the non-story thing that it names.
If we break up an aggregated story into its input elements, and continue to do so recursively, we will – after a finite number of steps – end up with a finite number of atomic stories. They constitute the elementary building blocks of our initial, aggregated story. As the discourse evolves, new things come into existence by being given new and unique names. A new thing therefore enters the discourse through its corresponding atomic story.
3. Stories as mappings between named things and situated expressions
The support of a story \, S \, – written \, S_{upp}(S) \, – is the set of things that are mentioned by \, S \, , i.e., the set of things that the story \, S \, ”is about”. Although the totality of \, T_{hings} \, is too large to form a set, the part \, S_{upp}(S) \, is a finite set of named things.
The expressions within a story \, S \, – written \, E_{xpr}(S) \, – are the ”substories” added by \, S \, , as well as the substories referred to from within \, S \, , i.e., the ”expressions of mentioning” within the stories over which \, S \, is (recursively) aggregating. \, E_{xpr}(S) \, is also a finite set of named things. However, it also carries additional structure because mentionings are situated. Within the same story, things are often mentioned several times – usually in substories that take place within different contexts.
In this way, a story \, S \, can be considered as a function from the set \, S_{upp}(S) \, to the set of all subsets of \, E_{xpr}(S) \, – denoted \, 2^{\, E_{xpr}(S)} \, . The story \, S \, maps every thing \, T \, in \, S_{upp}(S) \, to the set of substories of \, T \, – either within the additions of the story \, S \, itself, or within one of its recursively referenced substories. Since this set of mentionings of \, T \, forms a subset of \, E_{xpr}(S) \, , we can write:
\, S_{upp}(S) \ni T \mapsto \, the set of substories of \, S \, that mention \, T \, \in 2^{\, E_{xpr}(S)} .
Using postfix functional notation for storytelling, we can write this relationship as
\, S_{upp}(S) \ni T \mapsto (T)S \in 2^{\, E_{xpr}(S)} ,
where a thing \, T \, in \, S_{upp}(S) \, is mapped by \, S \, to the set of substories \, (T)S \, in \, 2^{\, E_{xpr}(S)} \, that mention \, T \, .
4. The Universal Discourse Graph
A discourse is a set of stories that are connected in some way. In order to model a specific discourse, it can be useful to represent it against a background of all the discourses that have ever taken place. These discourses form a (very large but finite) graph that we could call the Universal Discourse Graph ( \, U_{DG} \, ). The nodes of this graph consist of all the stories that have ever been told, and the arcs consist of the ”about-references” between them – showing which story is talking about what (see Figure 5).
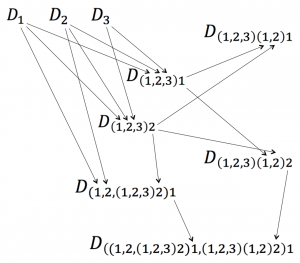
Figure 5: The Universal Discourse Graph
Imagine that we start as in Figure 5 with three atomic stories called \, D_1, D_2, D_3 . These atomic stories constitute the input to two aggregated stories \, D_{(1, 2, 3)1} \, respectively \, D_{(1, 2, 3)2} \, , which are about the same things, i.e., they have a common theme. Arrows are drawn from a story \, S \, to all the other stories that use \, S \, as input. Hence the numbers connected by arrows have the same identity and correspond to the same story.
Connecting back to the discussion in ch. 3.2 we can write:
\, T_{hings} \succ S_{upp}(U_{DG}) \supset S_{upp}(S) \rightarrow E_{xpr}(S) \subset E_{xpr}(U_{DG}) \prec T_{hings} \, .
Here the “curved inequality signs” indicate that \, T_{hings} \, is not a set – but somehow ”larger” (= more inclusive) than the sets that are smaller than it. The subset inclusions between the supports and expressions of \, S \, and the \, U_{DG} \, are valid if we think of the \, U_{DG} \, as becoming ”instantly updated” whenever a new story is created.
5. Genrefication – creating and dissolving genres
A genre is created by grouping together a number of stories that describe a common theme in common ways. Behind the creation of a genre lies an ambition to explore if the grouping together of the constituting stories into a genre could serve to increase the effectiveness and efficiency of the stories that describe this group in common ways.
For example, the stories \, D_{(T)1} \, and \, D_{(T)2} \, have the common theme \, D_{(T)} \, , and if they treat this theme in “common enough” ways, we can group them into a genre by writing
\, D_{(T)1}, D_{(T)2} = D_{(T)(1,2)} .
In Figure 5, the two stories \, D_{(1, 2, 3)1} \, and \, D_{(1, 2, 3)2} \, have been grouped into the genre \, D_{(1, 2, 3)(1,2)} \, which is the common theme of the two stories \, D_{(1, 2, 3)(1,2)1} \, and \, D_{(1, 2, 3)(1,2)2} . In this form of “story algebra,” the genrefication operator binds harder than the story operator. Hence the interpretation of \, D_{(1, 2, 3)(1, 2)1} \, should be \, D_{((1, 2, 3)(1, 2))1} \, and not \, D_{(1, 2, 3)((1, 2)1)} . In fact, the latter expression could be interpreted as having formed a genre from one single story, which seems to be a somewhat counter-intuitive (but not forbidden) thing to do.
A genre can be dissolved by using the genrefication operator in reverse. If the genre \, D_{(1, 2, 3)(1, 2)} \, has become obsolete, the story \, D_{(1, 2, 3)(1, 2)1} \, , which is about this obsolete genre, should then be reinterpreted as \, D_{((1, 2, 3)1, (1,2,3)2)1} \, , which is a story about the two separate stories \, D_{(1, 2, 3)1} \, and \, D_{(1, 2, 3)2} \, , which in turn have the common theme \, D_{(1, 2, 3)} \, but which do not treat them in “common-enough” ways to merit the formation of a genre.
6. The Universal Reference Graph
It is important to observe that stories are referencing each other “in reverse order” with respect to their “time order” (= order of creation), reflected in the arrows of Figure 5, since newer stories must by necessity be referencing older stories. Hence, by reversing the order of the arrows in Figure 5, we arrive at a reference-based representation of the corresponding discourse, which we will call the Universal Reference Graph ( \, U_{RG} \, ). Just as the \, U_{DG} \, reflects the order in which stories are created, the \, U_{RG} \, reflects the order in which stories are referencing each other.

Figure 6: The Universal Reference Graph
Each story \, S \, has a reference graph that consists of the sub-graph of stories that it is referencing (directly or indirectly – as encoded in the collection of meta-nomials of \, S \, with respect to each atomic story that \, S \, references. These are precisely the stories that can be reached by following the arrows that are starting from \, S \, to their “atomic” endpoints. The reference-based representation of the discourse of Figure 5 is depicted in Figure 6.
The reference graph of a story captures its aggregational structure down to the atomic story level. For example, the story \, D_{((1, 2, (1, 2, 3) 2) 1, (1, 2, 3) (1, 2) 2) 1} \, shown at the bottom of Figure 6 is aggregating over (= “is about” = “refers to”) the stories \, D_{(1, 2, (1, 2, 3) 2) 1} \, and \, D_{(1, 2, 3) (1, 2) 2} . The former of these stories is aggregating over the stories \, D_1, D_2 \, and \, D_{(1, 2, 3) 2} \, while the latter is aggregating over the genre \, D_{(1, 2, 3) (1, 2)} \, which in turn consists of the two stories \, D_{(1, 2, 3) 1} \, and \, D_{(1, 2, 3) 2} \, that have been grouped together. Carrying this de-aggregation (= dissection) process one step further, we see that we arrive at the atomic story level for all branches of the reference graph of the initial story.
7. Placifying a story within the URG
Sometimes it is desirable to consider a story \, S \, as “placed” (= embedded) within the \, U_{RG} \, , i.e., to consider the story \, S \, as a subgraph of the \, U_{RG} .
Every individual story corresponds to a subgraph of the \, U_{RG} \, . Moreover, every aggregated story \, S \, contains substories that correspond to subgraphs of the full ”story-graph” of \, S \, .
With respect to the discussion of the last section, if we want to consider a story \, S \, as a function on the entire \, S_{upp}(U_{RG}) \, – which represents everything that has ever been ”storified” (= expressed in a story) – the story \, S \, can be easily extended to cover all the things in \, S_{upp}(U_{RG}) \, by mapping the rest of the things (i.e., the things not discussed in the story \, S \, ) to the empty expression.
8. Paths of reference: the meta-nomial of a thing with respect to a story
If we think of a story about something as a meta-thing, we can introduce an interesting way to describe stories. Let us assume that the thing we are talking about is the mountain called ”Mount Everest”. Hence we can write, for example:
t_{hing} \, = the mountain called Mount Everest,
meta-thing = a story about the mountain called Mount Everest,
meta-meta-thing = a story about a story about the mountain called Mount Everest,
…
We can now introduce the meta-nomial of a t_{hing} \, with respect to a s_{tory} that references it:
t_{hing} \circ s_{tory} = t_{hing} ({\sum\limits_{p_{ath} \in p_{aths}}^{ \text {} }} m_{eta}^{|p_{ath}|}) s_{tory} \, .
The meta-nomial splits the refererence graph that connects the \, s_{tory} \, with the \, t_{hing} \, into different reference paths that lead from the \, s_{tory} \, to the \, t_{hing} . Each reference path is represented in the meta-nomial by a monomial (= term). The degree of this monomial is given by \, |p_{ath}| \, and it represents the number of references (= number of ”meta:s”) that lie between the \, s_{tory} \, and the \, t_{hing} \, along this specific \, p_{ath} .
In summary, the meta-nomial encodes the paths of reference of all the different ways that a given s_{tory} is referentially connected with a given \, t_{hing} . These paths of reference are embedded within the \, U_{RG} \, , which provides a background (= a space) upon which all possible stories can be positioned (= placified).
///////
Representation: \, [ \, p_{resentant} \, ]_{B_{ackground}} \, \mapsto \, \left< \, r_{epresentant} \, \right>_{B_{ackground}}
Reconstruction: \, \left( \, \left< \, r_{epresentant} \, \right>_{B_{ackground}} \, \right)_{B_{ackground}} \mapsto \,\, p_{resentant}
//////
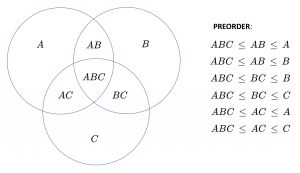
\, ABC \, AB \, BC \, AC, A \, B \, C \, .
Preorder:
\, ABC \, \leq \, AB \, \leq \, A \,
\, ABC \, \leq \, AB \, \leq \, B \,
\, ABC \, \leq \, BC \, \leq \, B \,
\, ABC \, \leq \, BC \, \leq \, C \,
\, ABC \, \leq \, AC \, \leq \, A \,
\, ABC \, \leq \, AC \, \leq \, C \,
///////
\, [ \, s_{ubject} \, ]_{ABC} \, \leq \, [ \, s_{ubject} \, ]_{AB} \, \leq \, [ \, s_{ubject} \, ]_{A} \,
\, [ \, s_{ubject} \, ]_{ABC} \, \leq \, [ \, s_{ubject} \, ]_{AB} \, \leq \, [ \, s_{ubject} \, ]_{B} \,
\, [ \, s_{ubject} \, ]_{ABC} \, \leq \, [ \, s_{ubject} \, ]_{BC} \, \leq \, [ \, s_{ubject} \, ]_{B} \,
\, [ \, s_{ubject} \, ]_{ABC} \, \leq \, [ \, s_{ubject} \, ]_{BC} \, \leq \, [ \, s_{ubject} \, ]_{C} \,
\, [ \, s_{ubject} \, ]_{ABC} \, \leq \, [ \, s_{ubject} \, ]_{AC} \, \leq \, [ \, s_{ubject} \, ]_{A} \,
\, [ \, s_{ubject} \, ]_{ABC} \, \leq \, [ \, s_{ubject} \, ]_{AC} \, \leq \, [ \, s_{ubject} \, ]_{C} \,
///////