This page is a sub-page of our page on Vector spaces.
///////
Related KMR pages:
• Shift of Basis (in general).
• Representation and reconstruction of vectors.
///////
Other relevant sources of information:
• Change of basis for a vector space
///////
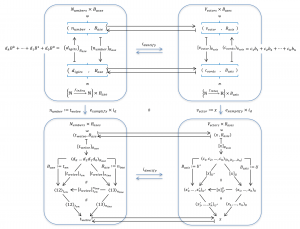
The Basis-Shift formula for Vectors
The Base-Shift formula for Numbers carries over verbatim to the Basis-Shift formula for Vectors, except for the replacement of the term \, B_{ase} \, by the term \, B_{asis} \, and the replacement of the term \, d_{igits} \, by the term \, c_{oordinates} \,.
It is often useful to have a symbolic name for the operation of shifting the \, B_{asis} \, of a \, v_{ector} \, from \, {B_{asis}}_1 \, to \, {B_{asis}}_2 \,. This operation will be called \, B_{asisShift} \, and its action on a given \, v_{ector} \, will be expressed in three different ways:
i) \, {[B_{asisShift}]}_{{B_{asis}}_2}^{{B_{asis}}_1} \, or
ii) \, {[v_{ector}]}_{{B_{asis}}_2}^{{B_{asis}}_1} \, if the \, B_{asisShift} \, operation is clear from the context, or
iii) \, {[\,\,\,]}_{{B_{asis}}_2}^{{B_{asis}}_1} \, if both the \, v_{ector} \, and the \, B_{asisShift} \, operation are clear from the context.
/////////
U \triangleq \begin{bmatrix} | & & | \\ u_1 & \cdots & u_m \\ | & & | \end{bmatrix}, \; U' \triangleq \begin{bmatrix} | & & | \\ u'_1 & \cdots & u'_m \\ | & & | \end{bmatrix} \, ,
///////
x \equiv \left( [x]_U \right)_U \equiv x_1 \, u_1 + \cdots + x_m \, u_m \equiv \left( [x]_{U'} \right)_{U'} \equiv x'_1 \, u'_1 + \cdots + x'_m \, u'_m \,Interpreting these relationships in matrix algebra leads to the matrix identities:
\, x \equiv U \begin{bmatrix} x_1 \\ \vdots \\ x_m \end{bmatrix} \equiv \begin{bmatrix} | & & | \\ u_1 & \cdots & u_m \\ | & & | \end{bmatrix} \begin{bmatrix} x_1 \\ \vdots \\ x_m \end{bmatrix} \equiv\,\;\; \equiv U' \begin{bmatrix} x'_1 \\ \vdots \\ x'_m \end{bmatrix} \equiv \begin{bmatrix} | & & | \\ u'_1 & \cdots & u'_m \\ | & & | \end{bmatrix} \begin{bmatrix} x'_1 \\ \vdots \\ x'_m \end{bmatrix} ,
and we arrive at the matrix equality:
[x]_U \equiv U^{-1}U'[x]_{U'} \, .
Hence, multiplying the (column) coordinate vector \, [x]_{U'} \, with the matrix \, U^{-1}U' \, gives the (column) coordinate vector \, [x]_U \, , and the matrix that shifts the basis of a vector space from \, U' \, to \, U \, is given by:
{[B_{asisShift}]}_U^{U'} \equiv U^{-1}U' \, .
In matrix algebra, we can therefore the express the operation of change of basis from \, U' \, to \, U \, as:
[x]_U \equiv {[B_{asisShift}]}_U^{U'} [x]_{U'} \, .
///////
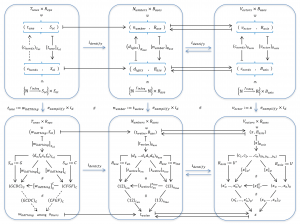
Shift of basis for vectors:
Assume that \, \mathbb{C}^m \, is an inner product space over the complex numbers \, \mathbb{C} \,
with the inner product given by \, x \cdot y = x_1 \overline{y_1} + \cdots + x_m \overline{y_m} \, for \, x, y \in \mathbb{C}^m .
Then we have the respective representations
\, [x]_B = { \left< \hat{x} \right> }_B = { \left< \begin{matrix} \hat{x}_1 \\ \vdots \\ \hat{x}_m \end{matrix} \right> }_B \, and \, [x]_{B'} = { \left< \hat{x'} \right> }_{B'} ={ \left< \begin{matrix} \hat{x'}_1 \\ \vdots \\ \hat{x'}_m \end{matrix} \right> }_{B'} ,
and the respective reconstructions
\, x = \left( [x]_B \right)_B = \hat{x}_1 \, b_1 + \cdots + \hat{x}_m \, b_m = \left( [x]_{B'} \right)_{B'} = \hat{x'}_1 \, b'_1 + \cdots + \hat{x'}_m \, b'_m .
In matrix notation, we can write
\, [x]_{B'} = [ \;\; ]_{B'}^B \, [x]_B .
\, [x]_B = [ \;\; ]_B^{B'} \, [x]_{B'} = [ \;\; ]_B^{B'} \, [ \;\; ]_{B'}^B \, [x]_B .
Hence we have
\, [ \;\; ]_B^{B'} \, [ \;\; ]_{B'}^B = I ,
where \, I \, is the identity matrix, and therefore
\, [ \;\; ]_B^{B'} = { [ \;\; ]_{B'}^B }^{-1} .
Now, if \, [ \;\; ]_{B'}^B \, is a unitary matrix, we have
\, { [ \;\; ]_{B'}^B }^{-1} = { [ \;\; ]_{B'}^B }^{*} ,
where the * denotes “complex transposition” of the matrix elements,
which means transposition of them accompanied by their complex conjugation.
///////
Representation and Reconstruction of Vectors 1:

///////
Change of basis for vectors:
///////
Numbers and Vectors are naturally related to each other:
Hence Numbers and Vectors are naturally equivalent.
Numbers and Vectors are naturally related to Music:
Check out our section on Category Theory
//////
The longer I read, the more the higher that your material is.
I have covered many of their additional sources, however, only here I have discovered valid advice with facts that are necessary to bear at heart.
I suggest that you publish articles with topics to upgrade mine specifically, our knowledge. The language is also brilliant! I really believe I have found my supply of their very up to date information, thanks to you!