This page is a sub-page of our page on Euclidean Geometry.
///////
Related KMR-pages:
• Linear Algebra
• The Mathematical Explainatorium
///////
The interactive simulations on this page can be navigated with the “the Fee Viewer of the Graphing Calculator“.
///////
Representation and Reconstruction of a Presentant against a certain Background
Representation: \, [ \, p_{resentant} \, ]_{B_{ackground}} \, \mapsto \, \left< \, r_{epresentant} \, \right>_{B_{ackground}}
Reconstruktion: \, \left( \, \left< \, r_{epresentant} \, \right>_{B_{ackground}} \, \right)_{B_{ackground}} \mapsto \,\, p_{resentant}
///////
Two perpendicular lines through the point (0, m) expressed in “slope form”:
\, [ \, l_{ine1} \, ]_{S_{lopeForm}} \, \mapsto \, \left< \; y = kx + m \; \right>_{S_{lopeForm}} .
This form can represent all lines in the plane except the linje \, x = 0 \, ,
which corresponds to an infinite value of the slope \, k .
The perpendicular line through the point (0, m) in slope form is given by
\, [ \, l_{ine2} \, ]_{S_{lopeForm}} \, \mapsto \, \left< \; y = (-\frac{1}{k})x + m \; \right>_{S_{lopeForm}} .
This form can represent all lines in the plane except the linje \, y = 0 \, ,
which corresponds to an infinite value of the slope \, k .
The interactive simulation the created this movie.
///////
Line in two-point form
This form can represent all lines in the plane.
Let \, A \, och \, B \, be two “dragable” points. In the Graphing Calculator a dragable point is represented by a complex number. The \, xy -coordinates of the points \, A \, och \, B \, are therfore given by \, (\mathrm{Re} \, A, \mathrm{Im} \, A) \, and \, (\mathrm{Re} \, B, \mathrm{Im} \, B) respectively.
The interactive simulation that created this movie.
///////
Two perpendicular lines through the origin in angular form
This form can represent all lines (in the plane) that pass through the origin.
\, [ \, l_{inje1} \, ]_{A_{ngularForm}} \, \mapsto \, \left< \; (x-a) \sin \phi - (y-b) \cos \phi = 0 \; \right>_{A_{ngularForm}} .
The perpendicular line through the point genom punkten \, (a, b) \, in angular form is given by
\, [ \, l_{inje2} \, ]_{A_{ngularForm}} \, \mapsto \, \left< \; (x-a) \cos \phi + (y-b) \sin \phi = 0 \; \right>_{A_{ngularForm}} .
The interactive simulation that created this movie.
///////
Two perpendicular lines through the origin in hyperplane form
The interactive simulation that created this movie.
///////
Two perpendicular lines through the point \, (a, b) \, in “affine-hyperplane form”
This form can represent all lines in the plane.
TERMINOLOGY:An affine hyperplane is a hyperplane that may be translated so that it does not necessarily pas through the origin – in contrast to a hyperplane which always passes through the origin.
In the Graphing Calculator a dragable point is represented by a complex number.
Introduce the variables \, a = \mathrm{Re} \, A \, and \, b = \mathrm{Im} \, A \, and let \, A \, be a dragable point.
Then the \, xy -coordinates of the point A \, A \, are given by \, (A_x, A_y) = (a, b) .
\, [ \, l_{inje1} \, ]_{A_{ffineHyperPlaneForm}} \, \mapsto \, \left< \; p (x-a) + q (y-b) = 0 \; \right>_{A_{ffineHyperPlaneForm}} .
Then the perpendicular line through the point \, (a, b) \, is given by:
\, [ \, l_{inje2} \, ]_{A_{ffineHyperPlaneForm}} \, \mapsto \, \left< \; q (x-a) - p (y-b) = 0 \; \right>_{A_{ffineHyperPlaneForm}} .
The interactive simulation that created this movie.
///////
Line through the point (Re A, Im A) perpendicular to the direction (Re B, Im B)
This form can represent all lines in the plane.
Let \, A \, and \, B \, be two dragable points. In the Graphing Calculator a dragable point is represented by a complex number. The \, xy -coordinates of the points \, A \, and \, B \, are therefore given by \, (A_x, A_y) = (\mathrm{Re} \, A, \mathrm{Im} \, A) \, respectively \, (B_x, B_y) = (\mathrm{Re} \, B, \mathrm{Im} \, B) .
The interactive simulation that created this movie.
///////
Linje through the point (Re A, Im A) along the direction (Re B, Im B) in parameter form
This form can represent all lines in the plane.
The interactive simulation that created this movie.
///////
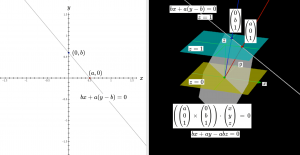
Euclidean points and lines in the plane are expressed in homogeneous coordinates
The Euclidean plane can be identified with the plane \, z = 1 \, in the Euclidean 3D-space.
This homogeneous form of coordinates can represent all Euclidean points and lines in the plane. Moreover, it also has exactly the necessary “space” needed to be able to represent a number of new points (called points “at infinity” “). All points at infinity have their \, z -coordinate equal to zero and must therefore lie on one and the same line (called “the line at infinity”). This line is represented by the 3D-plane \, z = 0 .
This form of representation leads to so-called projective geometry.
The intersection of the line at infinity with the \, x -axis has has the \, xy-coordinates \, (a,0) .
The intersection of the line at infinity with the \, y -axis has the \, xy -coordinates \, (0,b) .
///
\, \begin{pmatrix} a \\ 0 \\ 1 \end{pmatrix} \, , \, \begin{pmatrix} 0 \\ b \\ 1 \end{pmatrix} \,
\, \lgroup \begin{pmatrix} a \\ 0 \\ 1 \end{pmatrix} \times \begin{pmatrix} 0 \\ b \\ 1 \end{pmatrix} \rgroup \cdot \begin{pmatrix} x \\ y \\ z \end{pmatrix} \, = \, 0 \,
\, bx + ay - abz = 0 .
\, z = 0 .
///////
The interactive simulation that created this movie.
///////
///////