This page is a sub-page of the page on our review of the book Siffrorna i våra liv by Stefan Buijsman.
///////
Related KMR-pages:
• What is Mathematics?
• Math Book Reviews
• Geometric Algebra
• Clifford Algebra
• The Evolution of Geometric Arithmetic
///////
Other relevant sources of information:
///////
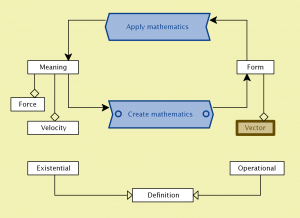
Sid 27, rad 9: Det är dessutom lite konstigt att matematiken går att använda till så mycket samtidigt som den är så oerhört abstrakt.
KOMMENTAR: Nej, det är inte så konstigt, eftersom abstraktionerna oftast har sin grund i strukturer som vi har iakttagit i verkligheten (t.ex. uppförandet hos meningsfulla (= tolkade) storheter som krafter och hastigheter). Det visar sig att dessa storheter uppvisar samma struktur vid sammansättning, dvs den s.k. ”kraftparallellogrammen” eller ”hastighetsparallellogrammen”, och denna strukturella likhet abstraherar vi till en “meningslös” storhet som vi kallar vektor. Vektorer kan vara VAD SOM HELST som uppfyller sammansättningslagarna, t.ex. både krafter och hastigheter. Vektorer definieras alltså INTE genom VAD DE ÄR utan genom HUR DE UPPFÖR SIG. Denna förskjutning är synnerligen viktig för att förstå de matematiska begreppens idéhistoria.
En vektor kan alltså vara vad som helst
– bara detta begrepp uppfyller formen för hur vektorer ska uppföra sig.
Detta är en synnerligen viktig poäng med ett begrepp som är fritt från mening – i betydelsen att man inte kan svara på frågan “vad är det?” Då kan man i stället fokusera på frågan “hur uppför det sig”, vilket i sin tur leder till följdfrågan “vad skulle det kunna vara (för begrepp) som uppför sig på detta sätt?” På detta vis har den matematiska utvecklingsprocessen under århundradenas – för att inte säga årtusendenas – gång utvidgat de matematiska begreppens abstrakta generalitet och därmed även deras konkreta tillämpningsområden.
///////
///////
///////
///////
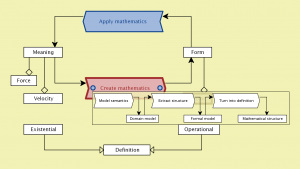
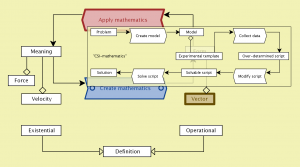
Abstraktionsprocessen går alltså från ”mening” till ”form” och meningen återfås sedan genom tillämpning (= tolkning) av symbolerna i formalismen. Poängen är, precis som i språket, att åstadkomma tankeekonomi. Har man t.ex. visat att något gäller för ”vektorer” så har man samtidigt visat att det gäller för både ”krafter” och ”hastigheter.”
Har man etablerat att ”varje fordon har en ägare” så har man etablerat detta faktum för bilar, båtar, flygplan, … utan att behöva upprepa sig för varje ”konkret” exempel på någon typ av ”fordon.”
///////
Från Mening till Form – Meningen med att vara Meningslös:
///////
Sid 90, rad 2: … så många berömda grekiska matematiker: Pythagoras, Euklides, Arkimedes, för att bara nämna de mest kända.
KOMMENTAR: Dessa namn är naturligtvis ’emblematiska’ men även Eudoxos bör nämnas här, framför allt som en skapande matematiker av första rangen. Euklides var framförallt nyskapande genom sitt sätt att framställa den matematiska information som fanns tillgänglig på hans tid (300-talet före Kristus). Eudoxus anses av många som den främste av de klassiska grekiska matematikerna, och den näst främste i hela antiken efter Arkimedes. Eudoxos gav viktiga bidrag till proportionsteorin, där han införde en definition som möjliggjorde en jämförelse mellan irrationella längder – på ett liknande sätt som vi idag använder oss av s.k. korsmultiplicering. Eudoxus teori beskrivs i Euklides Elementa. Definition 4 i denna bok kallas Eudoxus axiom och tillskevs honom av Arkimedes.
Det är svårt att överdriva betydelsen av Eudoxos proportionsteori eftersom den bygger upp en rigorös definition av rella tal. Detta gjorde det möjligt för talteorin att börja utvecklas igen – och vakna upp ur den förlamning som drabbat området efter pythagoréernas upptäckt av irrationella tal.
Ett annat fundamentalt bidrag från Eudoxos var hans arbete med integration. Där utvecklade han sin “uttömningsmetod” (eng: “method of exhaustion“) som byggde på proportionsteorins förmåga att jämföra irrationella tal. Om man hade en gissning om vad värdet av t.ex. klotets volym borde vara så kunde man bevisa om denna gissning var rätt eller fel med hjälp av uttömningsmetoden. Om t.ex. det gissade värdet var korrekt kunde man på detta sätt visa att det korrekta värdet varken var mindre eller större än det gissade.
///////
ANM: Eudoxos, Appolonius från Perga och Arkimedes var enligt mångas mening de tre största matematikerna från den grekiska antiken. Det vi vet om Pythagoras är endast fragment av berättelser i tredje och fjärde hand.
///////
Sid 92, rad 14: … så vet vi att Arkimedes var en enastående matematiker och att han framförallt bidrog med insikter om volymer och areor.
KOMMENTAR: Sådana insikter var en del av Arkimedes mångdimensionella geni. En annan mycket viktig del var integralkalylen. År 1906 återfanns ett manuskript av Arkimedes – kallat ”The Method” – som en s.k. palimpsest, dvs en skinnhud, där medeltidsmunkarna hade skrapat bort Arkimedes ursprungstext och ersatt den med kristna böner.
///////
Sid 47, rad 24: Grekerna kom inte mycket längre.
KOMMENTAR: Jo, det gjorde de, som t.ex. framgår av ovanstående avsnitt om Eudoxos och Arkimedes. Men, det är klart, de hade kunnat komma ännu längre. Det fanns dock en mycket viktig mental blockering som var svår att övervinna med den extremt klumpiga och svårhanterliga algebraiska notation som “de gamla grekerna” hade tillgång till.
De hade i själva verket början till en geometrisk algebra,
nämligen den yttre produkten \, \wedge \, . Deras algebra (i modern notation) fungerade så här:
\, l_{ängd} \wedge l_{ängd} \, \equiv \, y_{ta} \,
\, l_{ängd} \wedge l_{ängd} \, \wedge l_{ängd} \equiv \, v_{olym} \,
\, l_{ängd} \wedge l_{ängd} \, \wedge l_{ängd} \wedge l_{ängd} \equiv \, i_{ngenting} \,
eftersom det inte fanns mer än tre dimensioner på den tiden.
Den som ändrade på detta faktum var en tyskspråkig gymnasielärare i Stettin vid namn Hermann Günther Graßmann. År 1844 publicerade han sitt mästerverk Die Lineale Ausdehnungslehre, ein neuer Zweig der Mathematik [The Theory of Linear Extension, a New Branch of Mathematics]. Boken betecknas vanligen Ausdehnungslehre, vilket kan översättas som “utsträckningssteori” eller “teori för extensiva magnituder.”
I denna bok – som ingen läste eftersom den var skriven i en “obskyr filosofisk stil” som inga matematiker var vana vid – införde Graßmann abstrakta vektorrum med n-dimensionell algebra och geometri. Därmed skapade han det område vi idag kallar linjär algebra.
Under 1870-talet utvecklade William Kingdon Clifford en algebra – kallad Cliffordalgebra – vilken byggde på Graßmanns yttre algebra (på engelska kallad exterior algebra).
/////// Quoting Wikipedia on William Kingdon Clifford:
In 1878 Clifford published a seminal work, Applications of Grassmann’s extensive algebra, building on Grassmann’s algebraic work. He had succeeded in unifying the quaternions, developed by William Rowan Hamilton, with Grassmann’s outer product (also known as the exterior product). Clifford understood the geometric nature of Grassmann’s creation, and that the quaternions fit cleanly into the algebra Grassmann had developed. The versors in quaternions facilitate representation of rotation.
Clifford laid the foundation for a geometric product, composed of the sum of the inner product and Grassmann’s outer product. The geometric product was eventually formalized by the Hungarian mathematician Marcel Riesz. The inner product equips geometric algebra with a metric, fully incorporating distance and angle relationships for lines, planes, and volumes, while the outer product gives those planes and volumes vector-like properties, including a directional sensitivity.
Combining the two brought the operation of division into play. This greatly expanded our qualitative understanding of how objects interact in space. Crucially, it also provided the means for quantitatively calculating the spatial consequences of those interactions. The resulting geometric algebra, as Clifford called it, eventually realized the long sought goal[13] of creating an algebra that mirrors the movements and projections of objects in 3-dimensional space.[14]
Moreover, Clifford’s algebraic schema extends to higher dimensions. The algebraic operations have the same symbolic form as they do in 2 or 3-dimensions. The importance of general Clifford algebras has grown over time, while their isomorphism classes – as real algebras – have been identified in other mathematical systems beyond simply the quaternions.
The realms of real analysis and complex analysis have been expanded through the algebra H of quaternions, thanks to its notion of a three-dimensional sphere embedded in a four-dimensional space.
Quaternion versors, which inhabit this 3-sphere, provide a representation of the rotation group SO(3).
Clifford noted that Hamilton’s biquaternions were a tensor product H ⊗ C of known algebras, and proposed instead two other tensor products of H:
Clifford argued that the “scalars” taken from the complex numbers C might instead be taken from split-complex numbers D or from the dual numbers N. In terms of tensor products, H ⊗ D produces split-biquaternions, while H ⊗ N forms dual quaternions.
The algebra of dual quaternions is used to express screw displacement, a common mapping in kinematics.
/////// End of quote from Wikipedia (on William Kingdon Clifford)
Den geometriska produkten av två vektorer \, a \, och \, b \, “kodar för” både
deras grad av parallellitet och deras grad av ortogonalitet.
Definition: \, a \, b = a \cdot b + a \wedge b .
Se nedan för baselementen i algebran.
Den geometriska produkten är distributiv (både från vänster och från höger)
över multivektoraddition. Vänsterdistributiviteten ger:
\, a \, b \, = \, a \, ( b_{ \, \shortparallel} + b_{\perp} ) \, = \, a \, b_{\, \shortparallel} \, + \, a \, b_{\perp} \, = \, a \cdot b_{\, \shortparallel} + a \wedge b_{\, \shortparallel} + a \cdot b_{\perp} + a \wedge b_{\perp} \, = \,
\, = \, a \cdot b_{\, \shortparallel} + a \wedge b_{\perp} \, = \, a \cdot b + a \wedge b \,
som sig bör.
Högerdistributiviteten ger:
\, a \, b \, = \, ( a_{ \, \shortparallel} + a_{\perp} ) \, b \, = \, a_{ \, \shortparallel} \, b + a_{\perp} \, b \, = \, a_{ \, \shortparallel} \cdot b + a_{ \, \shortparallel} \wedge b + a_{\perp} \cdot b + a_{\perp} \wedge b \, = \,
\, = \, a_{ \, \shortparallel} \cdot b + a_{\perp} \wedge b \, = \, a \cdot b + a \wedge b \,
som sig bör.
///////
Vad en riktad magnitud kan uträtta
///////
Ett riktat segment kan peka ut en slutpunkt relativt en given startpunkt
Om startpunkten betraktas som “nollpunkt” får man en Euklidisk vektor, en s.k. riktningsvektor. Om startpunkten tas med får man en affin vektor (= en positionsvektor)
///////
En riktad plan yta kan lösa ekvationen \, x^2 \, = \, -1 \, utan imaginära storheter
NOTERA: Militären löser ekvationen \, x^2 \, = \, -1 \, utan att blanda in imaginära storheter:
(vänster om) (vänster om) utgångsriktningen = (vänster om)^2 utgångsriktningen =
= (helt om) utgångsriktningen = – utgångsriktningen.
(höger om) (höger om) utgångsriktningen = (höger om)^2 utgångsriktningen =
= (helt om) utgångsriktningen = – utgångsriktningen.
Operationerna “vänster om” och “höger om” fungerar alltså som de imaginära storheterna \, i \, och \, -i \, för komplexa tal. Vi kan åstadkomma samma sak med hjälp av Cliffordalgebra:
Låt \, \mathcal {R} \, vara en kommutativ ring med enhetselement och låt E vara en ändlig, totalordnad mängd, dvs E = \{e_1, \ldots, e_n\} där e_1 < e_2 < \ldots < e_n. Vi identifierar k –basbladen e_{n_1} e_{n_2} \ldots e_{n_k}, där n_1 < n_2 < \ldots < n_k \leq n, med k -delmängderna \{e_{n_1}, \ldots, e_{n_k}\} \subseteq E och vi betecknar enhetspseudoskalären e_1 e_2 \ldots e_n med E (genom en oproblematisk förändring av sammanhanget). Slutligen identifierar vi ringens enhet 1 med den tomma mängden \emptyset.
Vi betraktar Cliffordalgebran C_l(E) som den fria \mathcal {R} -modulen genererad av potensmängden \wp(E) av alla delmängder av E , dvs
\, C_l(E) \, = \, {\oplus \atop {e \, \in \, \wp(E) } } \mathcal {R}.
För multiplikationen i \, C_l(E) \, inför vi för baselementen räknereglerna:
\, e_i^2 \, = \, 1 \, för \, i = 1, ..., n , och
\, e_j \, e_i \, = \, - e_i \, e_j \, om \, i \neq j .
Dessa regler utvidgas sedan distributivt till alla multivektorer i C_l(E) .
Ett bevis för att ovanstående konstruktion verkligen ger en Cliffordalgebra finns i ett appendix till artikeln:
• Naeve, A., Svensson, L. (2001): Geo-MAP unification, in Geometric Computing with Clifford Algebras – Theoretical Foundations and Applications in Computer Vision and Robotics, Sommer, G. (ed.), pp. 105-126, Springer Verlag, ISBN 3-540-41198-4.
Om \, i \neq j \, får vi alltså:
\,( e_i \, e_j)^2 \, = \, e_i \, e_j \, e_i \, e_j \, = \, - e_j \, e_i \, e_i \, e_j \, = \, - e_j \, e_j \, = \, -1 ,
dvs \, e_i \, e_j \, löser ekvationen \, x^2 \, = \, -1 . Varje sådan bivektor fungerar alltså som en imaginär enhet.
///////
En riktad volym kan befria Jacobideterminanten från sin beloppsmässiga tvångströja
(vid variabelsubstitution i multipelintegraler):
///////
Den yttre produkten kan befria kryssprodukten från sin tredimensionella tvångströja
\, a \times b \, \stackrel {\mathrm{def}}{=} \, (a \wedge b) \, I^{-1}
där \, I = \, e_1 e_2 \cdots e_n \, är enhetspseudoskalären (= det riktade enhetsvolymselementet) för \, C_l(e_1, e_2, \cdots, e_n) \, .
///////
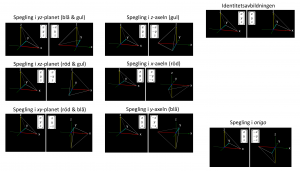
Speglingar i koordinatplan, i koordinataxlar och i origo
///////
Geometriska tal i den Euklidiska 3D-rymden:
\, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) \,
\, S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) \,
\, S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \,
och de motsatt riktade och ekvivalenta speglingsbeskrivningarna:
\, S_{{pegla}\,i\,P_{lan}} (B_{akåt}) \, = \, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) \,
\, S_{{pegla}\,i\,P_{lan}} (H_{ögeråt}) \, = \, S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) \,
\, S_{{pegla}\,i\,P_{lan}} (N_{edåt}) \, = \, S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \,
///////
Dualisering:
\, (F_{ramåt} V_{änsteråt})^{\star} \, = \, (F_{ramåt} V_{änsteråt}) \, {(- \, F_{ramåt} V_{änsteråt} U_{ppåt})}^{-1} \, = \,
\, = \, - \, F_{ramåt} V_{änsteråt} (U_{ppåt})^{-1} (V_{änsteråt})^{-1} (F_{ramåt})^{-1} \, =
\, = \, - \, F_{ramåt} V_{änsteråt} N_{edåt} H_{ögeråt} B_{akåt} \, = \, F_{ramåt} V_{änsteråt} H_{ögeråt} N_{edåt} B_{akåt} \, =
\, = \, F_{ramåt} N_{edåt} B_{akåt} \, = \, - \, F_{ramåt} B_{akåt} N_{edåt} \, = \, - \, N_{edåt} \, = \, U_{ppåt}
\, (V_{änsteråt} U_{ppåt})^{\star} \, = \, (V_{änsteråt} U_{ppåt}) \, {(- F_{ramåt} V_{änsteråt} U_{ppåt})}^{-1} \, = \,
\, = \, - V_{änsteråt} U_{ppåt} (U_{ppåt})^{-1} (V_{änsteråt})^{-1} (F_{ramåt})^{-1} \, = \, - (F_{ramåt})^{-1} \, = \, - B_{akåt} \, = \, F_{ramåt}
\, (F_{ramåt} U_{ppåt})^{\star} \, = \, (F_{ramåt} U_{ppåt}) \, {(- \, F_{ramåt} V_{änsteråt} U_{ppåt})}^{-1} \, = \,
\, = \, - \, F_{ramåt} U_{ppåt} (U_{ppåt})^{-1} (V_{änsteråt})^{-1} (F_{ramåt})^{-1} \, =
\, = \, - \, F_{ramåt} H_{ögeråt} B_{akåt} \, = \, F_{ramåt} B_{akåt} H_{ögeråt} \, = \, H_{ögeråt} \, = \, - V_{änsteråt}
///////
Speglingar i plan, linjer och punkter
Tre vinkelräta planspeglingar ger en spegling i planens skärningspunkt (= origo):
\, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \, = S_{{pegla}\,i\,P_{unkt}} (O_{rigo}) \, = -1 \,
En spegling i en linje är lika med en halvtvarvsrotation kring denna linje:
\, S_{{pegla}\,i\,L_{inje}} (e_{nLinje}) \, = \, R_{otera(H{alvt}V_{arv})\,k_{ring}} (d_{ennaLinje}) \,
Två vinkelräta planspeglingar ger en halvtvarvsrotation kring planens skärningslinje:
\, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) \, = \, S_{{pegla}\,i\,L_{inje}} (L_{inje}(F_{ramåt} V_{änsteråt})^{\star}) \, = \, R_{otera(H{alvt}V_{arv})\,k_{ring}} (L_{inje} (U_{ppåt})) \,
\, S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \, = \, S_{{pegla}\,i\,L_{inje}} (L_{inje}(V_{änsteråt} U_{ppåt})^{\star}) \, = \, R_{otera(H{alvt}V_{arv})\,k_{ring}} (L_{inje} (F_{ramåt})) \,
\, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \, = \, S_{{pegla}\,i\,L_{inje}} (L_{inje}(F_{ramåt} U_{ppåt})^{\star}) \, = \, R_{otera(H{alvt}V_{arv})\,k_{ring}} (L_{inje} (H_{ögeråt})) \,
Dessutom har vi sambanden:
\, S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) S_{{pegla}\,i\,P_{lan}} (F_{ramåt}) \, = \, 1 \,
\, S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) S_{{pegla}\,i\,P_{lan}} (V_{änsteråt}) \, = \, 1 \,
\, S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) S_{{pegla}\,i\,P_{lan}} (U_{ppåt}) \, = \, 1 \,
///////
Speglingar i plan:
Sats: Låt \, P \, vara ett plan i \, {\mathbb{R}}^3 \, med enhetsnormalen \, n .
En spegling \, S_{P} \, i planet \, P \, kan i Geometrisk Algebra representeras så här:
\, {\mathbb{R}}^3 \ni x \mapsto - \, n \, x \, n \, = \, \bar{x} = S_{P}(x) \in {\mathbb{R}}^3 .
Bevis:
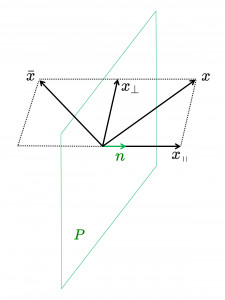
Spegling av vektorn \, x \, i planet \, P \, med enhetsnormal \, n \, kan uttryckas som:
\, \bar{x} \, = \, - \, n \, x \, n \, = \, - \, n \, (x_{\, \shortparallel} + x_{\perp}) \, n \, = \, - \, n \, x_{\, \shortparallel} \, n - \, n \, x_{\perp} \, n \, = - \, n \, n \, x_{\, \shortparallel} + n \, n \, x_{\perp} \, = \, - \, x_{\, \shortparallel} + x_{\perp} \, = \, S_{P} (x) \,
vilket avslutar beviset.
Rotationer
Två planspeglingar ger en rotation kring planens skärningslinje.
Allmänna rotationer kan uttryckas genom att använda versorer.
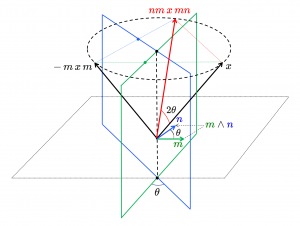
Låt det första respektive andra speglingsplanet ha enhetsnormalerna \, m \, respektive \, n .
Om vi tillämpar planspeglingslagen två gånger får vi:
\, \bar {\bar{x}} \, = \, - \, n \, ( - \, m \, x \, m ) \, n \, = \, n m \, x \, m n \,
Den algebraiska och geometriska strukturen hos en versor:
/////// Quoting Wikibooks Associative Composition Algebra / Division quaternions:
Lemma 1: Om \, a \, och \, b \, är kvadratrötter ur minus ett och om \, a \perp b så är \, a \, b \, a \, = \, b \, .
Bevis: \,\; 0 \, = \, a \, (a \, b + b \, a) \, = \, a^2 \, b + a \, b \, a \, = \, -b + a \, b \, a \, .
Lemma 2: Under samma hypotes är \, a \perp a \, b \, och \, b \perp a \, b \, .
Bevis (av att \, a \perp a\, b) \, : \, a \, (a \, b) + (a \, b) \, a \, = \, -b + a \, b \, a \, = \, 0 \, .
Låt \, u = e^{\, \theta \, \mathbf{r}} \, vara en versor. Det finns en gruppverkan (group action) på \, \mathbb{H} \, som bestäms av \, u \, :
Inner automorphism \, f \, : \, \mathbb{H} \, \ni \, q \, \mapsto \, u^{-1} q \, u \, \in \, \mathbb{H} \, .
Notera att \, u \, kommuterar med alla vektorer i planet \, \{\, x + y \, \mathbf{r} \, : \, x, y \, \in \, \mathbb{R} \, \} .
Välj nu \, \mathbf{s} \, från storcirkeln på \, \mathbb{S}^2 \, som är vinkelrät mot \, \mathbf{r} . Då är \, \mathbf{r} \, \mathbf{s} \, \mathbf{r} \, = \, \mathbf{s} \, enligt lemma 1. Beräkna nu \, f(\mathbf{s}) \, :
\;\;\;\;\;\;\;\;\;\;\;\; = \, ({\cos}^2 \theta - {\sin}^2 \theta) \, \mathbf{s} + (2\sin \theta \cos \theta) \, \mathbf{s} \, \mathbf{r} \, = \, \mathbf{s} \, \cos 2 \theta + \mathbf{s} \, \mathbf{r} \, \sin 2 \theta ,
vilket är en rotation med vinkeln \, 2 \theta \, i \, (\mathbf{s}, \mathbf{s} \, \mathbf{r}) \, planet.
Denna egenskap hos \, \mathbb{H} , att det finns en inre automorfi \, f \, som producerar rotationer, har visat sig vara mycket användbar.
/////// End of quote from Wikibooks
Två \, \theta -separerade speglingar ger en \, 2 \theta -separerad rotation:
I planet rör det sig om speglingar i linjer och i 3D-rymden rör det sig om speglingar i plan.
///////
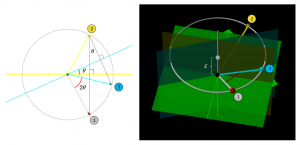
Verkan av en fix versor på en roterande vektor:
Filmen visar den rödmärkta vektorn, vars spets roterar kring den grå cirkeln. Varje position av denna vektor speglas först i den horisontella gula linjen (i det vänstra fönstret) med motsvarande spegling i det vertikala gula planet (i det högra fönstret), vilket resulterar i den gula vektorn.
Denna vektor speglas sedan i den ljusblå linjen (i det vänstra fönstret) med motsvarande spegling i det vertikala ljusblåa planet (i det högra fönstret), vilket resulterar i den ljusblåa vektorn.
Eftersom den ljusblåa vektorn är relaterad med den “rödnästa” vektorn via en konstant rotation, så följer det att den ljusblåa vektorn följer den rödnästa vektorn – på konstant avstånd och med konstant vinkel – runt den cirkulära kon vars symmetriaxel är identisk med \, z -axeln.
///////
Verkan av en variabel versor på en fix vektor:
Variationen av versorn orsakas av en förändring av vinkeln mellan den gula linjen och den ljusblå linen (i det vänstra fönstret) och därmed av motsvarande vinkel mellan det gula vertikala planet och det ljusblå vertikala planet (i det högra fönstret).
///////