This page is a sub-page of the page on our review of the book Siffrorna i våra liv by Stefan Buijsman.
///////
Related KMR-pages:
• Calculus
• Calculus of One Real Variable
• Calculus of Several Real Variables
• Calculus of One Complex Variable
In Swedish:
///////
Kap 5: Förändringsteori, vilket är liktydigt med differential- och integralkalkyl (ofta även kallad infinitesimalkalkyl), handlar om olika typer av samspel mellan “differentiering”, “derivering” och “integrering” av olika sorters funktioner med olika sorters egenskaper med olika grader av mjukhet med avseende på olika sorters måttstockar och mätmetoder.
En formelfri beskrivning av sådana samspel kompliceras av olika typer av språkliga inkongruenser, som till exempel det faktum att den operation som beräknar en funktions “derivata” på engelska kallas “att differentiera” (= “to differentiate”) funktionen.
På svenska gör vi alltför ofta misstaget att följa den engelska terminologin i stället för att utnyttja det svenska språkets möjligheter till språklig benämningskongruens mellan substantiv och verb, som när vi kallar den process som producerar en ‘derivata’ för ‘derivering’.
////////// MODIFIERA
En trolig effekt av denna språkliga inkongruens är att Buisman likställer begreppen ‘differential’ och ‘derivata’, vilket omöjliggör en mer preciserad diskussion omkring samspelet mellan dessa grundläggande begrepp. Därmed blir det svårt för honom att ta upp det viktigaste sambandet inom differential- och integralkalkylen, den s.k. fundamentalsatsen som säger att:
En tillräckligt ‘välartad’ funktion av en reell variabel
kan uttryckas både som
integralen av sin differential och som
derivatan av sin integral.
Mera precist uttryckt:
En differentierbar funktions värde i en punkt kan uttryckas som
(1): integralen upp till denna punkt av funktionens differential
över alla punkter vars värde är mindre än eller lika med värdet i denna punkt.
(2): derivatan i denna punkt av av funktionens integral
över alla punkter vars värde är mindre än eller lika med värdet i denna punkt.
NOTERA: För att uttrycksform (2) ska vara giltig krävs endast att funktionen är kontinuerlig,
eftersom dess integral i så fall automatiskt blir differentierbar.
///////
Vi inför nu en ‘otraditionell’ beteckning genom att definiera:
\, \stackrel{\, x}{\intop} df \,\, \stackrel {\mathrm{def}}{=} \, {{\int} \atop { (\;\,) \, \leq \, x}} \, df(\;\,) \, \equiv \, {{\int} \atop {(\;\,) \, \leq \, x}} \, f'(\;\,) \, d(\;\,) \,
där funktionen kallas \, f \, och den undersökta punkten kallas \, x .
Då kan vi uttrycka fundamentalsatsens innehåll så här:
(1): \, f(x) \, \equiv \, \stackrel{\, x}{\intop}df \, \, \equiv \, {{\int} \atop { t \, \leq \, x}} f'(t) \, dt ,
(2): \, f(x) \equiv \, {\frac{d}{du}|_{u=x} } \, ( \stackrel{\, u}{\intop} f ) \, .
• The fundamental theorem of calculus
///////
Ersättande av variabelnamn med markörer för gemensam input:
Namnen på variablerna saknar betydelse. Det viktiga är att det ska stå samma sak i de böjda paranteserna och (inbördes) samma sak i de raka paranteserna nedan. Varje parantestyp fungerar alltså som en anonym markör för gemensam input på alla ställen där denna parantestyp förekommer i uttrycket.
Vi kan nu beskriva fundamentalsatsens innehåll på ett ‘variabelnamnsfritt’ sätt:
(1): \, f[\;\,] \, \equiv \, \stackrel{\, [\;\,]}{\intop}df \,\, \equiv \, {{\int} \atop { (\;\,) \, \leq \, [\;\,]}} \, df(\;\,) \, \equiv \, {{\int} \atop {(\;\,) \, \leq \, [\;\,]}} \, f'(\;\,) \, d(\;\,) ,
(2): \, f[\;\,] \equiv \, {\frac{d}{d {(\;\,)}}|_{(\;\,)=[\;\;]} } \, ( \stackrel{\, (\;\,)}{\intop} f ) \, .
///////
De synonyma begreppen ‘primitiv funktion’, ‘obestämd integral’ och ‘antiderivata’:
Givet en funktion \, f \, . En funktion \, F \, kallas en primitiv funktion till \, f \,
om funktionen \, F \, har funktionen \, f \, som derivata, dvs om \, F' \, \equiv \, f .
NOTATION: Mängden av primitiva funktioner till \, f \, betecknas \, \intop f \, .
Eftersom derivatan av en funktion är noll om och endast om funktionen är konstant
har vi likheten \, \intop f \, \equiv \, F + c \, , där \, c \, är en godtycklig konstant, och vi kan skriva
\, (\intop f)' \, \equiv \, f \, , dvs
derivatan av den obestämda integralen av en funktion är lika med funktionen själv.
///////
Infinitesimalkalkylens fundamentalsats:
Fundamentalsatsen säger alltså att
en differentierbar funktion av en reell variabel
kan uttryckas både som
(1) integralen av sin differential, och som
(2) derivatan av sin integral.
///////
Likheterna (3) och (4) nedan beskriver fundamentalsatsuttryckens uppförande under variabelbyte. Detta är viktigt att förstå eftersom variabelbyte är en ofta förkommande metod för att förenkla integraluttryck.
(3): \, f(x) \, \equiv \, \stackrel{\, x}{\intop} df \, \equiv \, {{\int} \atop {u \, \leq \, x}} \, df(u) \, \equiv \, {{\int} \atop {u \, \leq \, x}} \, f'(u) \, du \, ,
(4): \, f(x) \equiv \, {\frac{d}{du}} |_{u=x} \, ( \stackrel{\, u}{\intop} f ) \, \equiv \, {\frac{d}{du}} |_{u=x} \, ( \, {{\int} \atop {t \, \leq \, u}} \, f(t) \, ) \, .
Här visar Leibniz notation sin oerhörda och hittills oöverträffade styrka, den styrka som gör att vi använder hans notation än idag.
ANM: En funktion av en variabel är deriverbar om och endast om den är differentierbar. Däremot kan en funktion av flera variabler vara deriverbar i varje variabel för sig (den kallas då partiellt deriverbar) utan att därför vara differentierbar. Differentierbarhet hos en funktion av flera variabler är därför ett starkare krav än deriverbarhet hos funktionen i varje variabel för sig.
///////
Variabelsubstitution i integraler
Reellvärda funktioner av en reell variabel representerar transformationer från en linje till en linje. Ett linjesegment, så som t.ex. \, \Delta x \, och därmed även \, dx , kan tillordnas en koordinatoberoende riktning, dvs en riktning som är oberoende vilken koordinatrepresentation som används på linjen ifråga.
Med hjälp av den vanliga kommutativa algebran är det däremot omöjligt att tilldela koordinatoberoende riktningar till geometriska objekt som har dimension större än ett, som t.ex. plan och volymer.
Detta är orsaken till en mycket viktiga skillnad som beskrivs nedan (under rubriken “viktig begränsning”) mellan Riemannintegraler som beror av en variabel
och Riemannintegraler som beror av flera variabler.
///////
En variabel:
\, \begin{matrix} \mathbf{R} & \xleftarrow{{{\int} \atop {D}}} & \mathbf{R} & \xleftarrow{f} & \mathbf{R}^1 & \xleftarrow{x} & \mathbf{R}^1 \\ & & & & & & & \\ {{\int} \atop {D}} f(x) dx & \longleftarrow & f(x) & \longleftarrow & x & & \\ & & & & & & & \\ & & & & D & & \\ & & & & & & & \\ {{\int} \atop {x^{-1}(D)}} f(x(u)) \det x'(u) \, du & \longleftarrow & f(x(u)) & \longleftarrow & x(u) & \longleftarrow & u \\ & & & & & & & \\ & & & & & & {x^{-1}(D)} \\ \end{matrix} \,
De två integralerna till vänster är lika med varandra, men de använder sig av olika sätt att beräkna resultatet. Därmed kan vi formulera:
Substitutionsformeln för att ändra den “löpande variabeln”
i en endimensionell Riemannintegral:
\, {{\int} \atop {D}} f(x) \, dx \, = \, {{\int} \atop {x^{-1}(D)}} f(x(u)) \det x'(u) \, du \, .
///////
Flera variabler:
\, \begin{matrix} \mathbf{R} & \xleftarrow{{{\int \cdots \int} \atop {D}}} & \mathbf{R} & \xleftarrow{f} & \mathbf{R}^n & \xleftarrow{x} & \mathbf{R}^n \\ & & & & & & & \\ {{{\int \cdots \int}} \atop {D}} f(x) \, dx & \longleftarrow & f(x) & \longleftarrow & x & & \\ & & & & & & & \\ & & & & D & & \\ & & & & & & & \\ {{\int \cdots \int} \atop {x^{-1}(D)}} \,\, f(x(u)) \, | \det x'(u) | \, du & \longleftarrow & f(x(u)) & \longleftarrow & x(u) & \longleftarrow & u \\ & & & & & & & \\ & & & & & & {x^{-1}(D)} \\ \end{matrix} \,I två dimensioner representerar \, dx \, = \, dx_1 \, dx_2 \, en infinitesimal, oriktad yta (dvs ett icke-riktat 2-volymselement), och i tre dimensioner representerar \, dx \, = \, dx_1 \, dx_2 \, dx_3 \, en infinitesimal, oriktad volym (dvs ett oriktat 3-volymselement), och så vidare …
I det flerdimensionella fallet svarar den endimensionella derivatan mot den så kallade Jacobimatrisen:
\, x'(u) \, = \, \begin{pmatrix} \frac{\partial x_1}{\partial u_1} & \frac{\partial x_1}{\partial u_2} & \cdots & \frac{\partial x_1}{\partial u_n} \\ \frac{\partial x_2}{\partial u_1} & \frac{\partial x_2}{\partial u_2} & \cdots & \frac{\partial x_2}{\partial u_n} \\ & & \ddots & \\ \frac{\partial x_n}{\partial u_1} & \frac{\partial x_n}{\partial u_2} & \cdots & \frac{\partial x_n}{\partial u_n} \end{pmatrix} \, ,
och tecknet hos den endimensionella derivatan motsvarar tecknet hos Jacobimatrisens determinant \, \det x'(u) .
///////
Den “obekväma sanningen” om Riemannintegralen i flera variabler:
Oriktade volymselement:
\, {{\int \cdots \int} \atop {D}} f(x) \, dx \, = \, {{\int \cdots \int} \atop {x^{-1}(D)}} f(x(u)) \, | \det x'(u) | \, du \, .
\, \textcolor{red}{ Viktig \, begränsning \, för \, Riemannintegraler \, i \, flera \, variabler } \, :
Denna formel är enbart giltig om determinanten \, \det x'(u) \, av Jacobimatrisen \, x'(u) \, inte ändrar tecken inom integrationsområdet \, D .
Exempel (i två variabler):
\, {{\iint} \atop {D}} f(x) \, dx_1 \, dx_2 = {{\iint} \atop {x^{-1}(D)}} f(x(u)) \; \vert \det \begin{pmatrix} \frac{\partial x_1}{\partial u_1} & \frac{\partial x_1}{\partial u_2} \\ \frac{\partial x_2}{\partial u_1} & \frac{\partial x_2}{\partial u_2} \end{pmatrix} | \; du_1 \, du_2 \, ,
under förutsättning att determinanten inte ändrar tecken inom integrationsområdet \, D .
///////
Förstärkning av algebran: riktade volymselement:
Genom att använda så kallad yttre algebra kan vi introducera riktade volymselement
och skriva \, dx \, = \, dx_1 \wedge dx_2 \, i två dimensioner, \, dx \, = \, dx_1 \wedge dx_2 \wedge dx_3 \, i tre dimensioner, och så vidare.
Den riktningskänsliga (= paritets-känsliga) integral som erhålles på detta sätt har många fördelar jämfört med den vanliga, riktningsokänsliga Riemannintegralen i flera variabler. Den viktigaste fördelen är att man inte behöver veta på förhand var Jacobimatrisen \, x'(u) \, ändrar tecken på sin determinant.
/////// Quoting Wikipedia (Exterior derivative)
On a differentiable manifold, the exterior derivative extends the concept of the differential of a function to differential forms of higher degree. The exterior derivative was first described in its current form by Élie Cartan in 1899; it allows for a natural, metric-independent generalization of Stokes’ theorem, Gauss’s theorem, and Green’s theorem from vector calculus.
If a k-form is thought of as measuring the flux through an infinitesimal k-parallelotope, then its exterior derivative can be thought of as measuring the net flux through the boundary of a (k + 1)-parallelotope
Översatt till Svenska:
På en differentierbar mångfald, utvidgar den exteriöra derivatan begreppet differentialen av en funktion till differentialformer av högre ordning. Den exteriöra derivatan introducerades i sin nuvarande form av Élie Cartan år 1899. Den möjliggör en naturlig, metrik-oberoende generalisering av Stokes teorem, Gauss’ teorem, and Green’s sats från vektoranalysen.
En k-form kan betraktas som ett mått på flödet genom en infinitesimal k-parallellepiped. I så fall kan k-formens exteriöra derivata betraktas som ett mått på nettoflödet genom randen till en (k + 1)-parallellepiped.
/////// End of Quote from Wikipedia
En stor fördel med detta synsätt är att det inte beror av dimensionen. I många vanliga tillämpningar är integrationsområdet \, \Omega \, ett \, n -dimensionellt område och \, \partial \Omega \, är dess \, (n-1) -dimensionella rand.
Genom att tillämpa den generaliserade Stokes sats på integraler över endimensionella reellvärda funktioner, där randen av ett intervall blir den formella skillnaden mellan dess två ändpunkter, dvs \, \partial [a, b] = b - a \, , erhålls infinitesimalkalkylens fundamentalsats (som framgår nedan).
///////
Exempel (i två variabler):
\, {{\iint} \atop {D}} f(x) \, dx_1 \wedge dx_2 \, = \, {{\iint} \atop {x^{-1}(D)}} f(x(u)) \, \det \begin{pmatrix} \frac{\partial x_1}{\partial u_1} & \frac{\partial x_1}{\partial u_2} \\ \frac{\partial x_2}{\partial u_1} & \frac{\partial x_2}{\partial u_2} \end{pmatrix} du_1 \wedge du_2 \, .
In fact, this type of integral, which is used in so-called geometric calculus, transforms exactly the same way as a one-dimensional integral under substitution. Therefore the one-dimensional integration-variable-substitution formula becomes valid in several variables without any restrictions on the sign of the determinant, dvs:
Variabelsubstitutionsformeln
\, {{\iint} \atop {D}} f(x) \, dx \, = \, {{\iint} \atop {x^{-1}(D)}} f(x(u)) \, \det x'(u) \, du \,
är giltig i hela integrationsområdet utan några inskränkningar.
///////
Inskränkningar som följer av att behöva hålla reda på
var Jacobideterminanten ändrar tecken :
Om samma riktningsokänsliga situation som för Riemannintegraler av flera variabler skulle behöva tillämpas på Riemannintegraler av en variabel, så skulle vi, för att integrera en differentierbar funktion \, f : \, \mathbb{R} \rightarrow \mathbb{R} , behöva veta på förhand var derivatan av \, f \, ändrar tecken. Denna derivata är nämligen den endimensionella versionen av Jacobimatrisen \, f'(x) \, – dvs det reella talet \, f'(x) \, måste betraktas både som en \, 1 \times 1-matris och som determinanten av denna matris. Tecknet på \, f'(x) \, är därmed den endimensionella versionen av Jacobideterminantens tecken.
Under sådana “riktningsokänsliga omständigheter” vore det därför omöjligt att integrera en funktion av en variabel över ett intervall där funktionens derivata ändrar tecken. Denna inskränkning skulle medföra en stor begränsning vad gäller användningsmöjligheterna av endimensionella Riemannintegraler.
///////
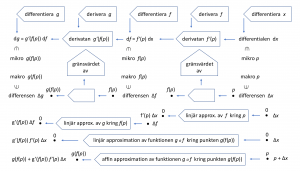
Kedjeregeln
Att omväxlande differentiera och derivera länkarna i en sammansättningskedja av funktioner resulterar i den s.k. kedjeregeln (the chain rule) – en av infinitesimalkalkylens viktigaste räknelagar. Om vi utgår från sammansättningen \, (g \circ f)(x) \, \equiv \, g(f(x)) \, får vi
diagrammet:
///////
Ovanstående begreppsanalys har visat att det är svårt att beskriva skillanderna mellan begreppen “differential” och “derivata” på ett formelfritt sätt och att det antagligen är därför som författaren valt att inte blanda in fundamentalsatsen i sin beskrivning av differentialer och integraler. Detta får negativa effekter på hans beskrivning av osäkerhetsteorins utveckling i kapitlel 6, vilket framgår av min webbsida om Osäkerhetsteori.
För att undvika begreppsförvirring påminner vi om engelskans språkliga inkongruens:
When we differentiate a function
we are in fact computing the function’s derivative.
Därför är det högst förståeligt att begreppen differential och derivata ofta blandas ihop med varandra. På engelska betyder som sagt verbet differentiate (i matematisk mening) att beräkna derivatan av en funktion. Denna språkliga inkongruens beror på att termen “derive” har en helt annan betydelse på engelska än den som termen “derivera” har på svenska.
Det är värt att notera att Wiktionary INTE har blandat ihop begreppen.
Där påstås (korrekt) att differentiera en funktion betyder att beräkna dess differential.
///////
Den resulterande derivatan kallas lutning eller förändringshastighet i det endimensionella fallet och matrisderivata, totalderivata, Fréchetderivata, funktionalmatris eller Jacobimatris i det flerdimensionella fallet.
Fundamentalsatsen formulerades och bevisades första gången (för specialfallet monotona funktioner) av James Gregory (1638–1675) i hans bok Geometriae Pars Universalis från 1668. Isaac Barrow (1630–1677) utvidgade huvudsatsen till en större klass av funktioner och hans student Isaac Newton (1642–1727) kompletterade utvecklingen av den underliggande teorin och metodiken för den framväxande infinitesimalkalkylen. Newton skrev ner sina ideer i ett manuskript som han kallade Method of Fluxions. Manuskriptet var färdigt 1671 men publicerades inte förrän 1736 – nästan tio år efter Newtons död.
Oberoende av Newton utvecklade Gottfried Wilhelm von Leibniz (1646–1716) sin egen version av infinitesimalkalkylen – inklusive en oerhört finurlig notation som väsentligen är i bruk än idag.
///////
Två generaliseringar av fundamentalsatsen
Inom vektoranalysen finns en generalisering av fundamentalsatsen som kallas Kelvin–Stokes sats. Den säger att ytintegralen av rotationen av ett vektorfält \, F \, över en yta i det Euklidiska rummet är lika med linjeintegralen av vektorfältet \, F \, över ytans rand.
Innom differentialgeometrin finns en generalisering av Kelvin-Stokes sats som kallas (den generaliserade) Stokes sats. Den handlar om integration av differentialformer över mångfalder. Den generaliserade Stokes sats både förenklar och generaliserar ett antal olika satser inom vektoranalysen.
Den generaliserade Stokes sats säger att integralen av en differentialform \, \omega \, över randen till en orienterbar mångfald \, \Omega \, är lika med integralen av dess “exteriöra derivata” \, d \omega \, över hela \, \Omega , i.e.,
\, _{\partial \Omega}^{ \;\, \int} \; \omega \, \equiv \, _{\Omega}^{ \, \int} \; d \omega \, .
TERMINOLOGI: Vi använder här den egna översättningen “exteriör derivata” av den engelska termen “exterior derivative”, eftersom den språkligt sett naturliga översättningen “yttre derivata” oftast har en annan betydelse på svenska.
///////
Den klassiska fundamentalsatsen formulerad via Stokes sats:
Låt \, F \, vara en s.k. primitiv funktion (= antiderivata = obestämd integral) till funktionen f .
Detta betyder per definition att \, F' \equiv f .
Med hjälp av Stokes’ sats får vi:
Integralen av en funktion \, f \, över ett intervall \, [a, b] \, är lika med
integralen av funktionen \, F \, över randen till intervallet \, [a, b] .
Enligt ovan är \, \partial [a, b] \, \equiv \, b - a , vilket ger:
\, \int_{a}^{b} f(x)dx \, \equiv \, _{[a, b]}^{ \;\;\, \int} \; F'(x)dx \, \equiv \, _{[a, b]}^{ \;\;\, \int} \; dF \, \equiv \, _{\partial [a, b]}^{ \;\;\;\, \int} \; F \, \equiv \, F(b) - F(a) .
För en differentierbar funktion \, f \, kan vi formulera fundamentalsatsen så här:
\, \int_{a}^{b} f'(x)dx \, \equiv \, _{[a, b]}^{ \;\;\, \int} \; df \, \equiv \, _{\partial [a, b]}^{ \;\;\;\, \int} \; f \, \equiv \, f(b) - f(a) \, .
///////
Homologi och Kohomologi
Låt \, \Omega \, vara ett orienterbart område och låt \, \partial beteckna randoperatorn, dvs avbildningen
\, \partial \, : \Omega \, \mapsto \, \partial \Omega .
Det är ett viktigt geometriskt faktum att randen av randen till ett orienterbart område alltid är lika med noll. Detta betyder att
\, \partial \circ \partial \;\; \Omega \, \stackrel {\mathrm{def}}{=} \, \partial(\partial \Omega) \, \equiv \, 0 \,
dvs \, \partial \circ \partial \equiv \, 0 .
Varje operator som sammansatt med sig själv är lika med noll ger upphov till ett kedjekomplex (eng. chain complex) med sin egen homologi och kohomologi.
///////
En kombinatorisk variant av Stokes sats finns beskriven i:
Naeve, A. & Svensson L., (1999), Discrete Integration and the Fundamental Theorem, The 5:th International Conference on Clifford Algebras and their Applications in Mathematical Physics, Ixtapa-Zihuatanejo, Mexico, June 27 – July 4, 1999.
///////
En intressant visuell representaton av differentialformer (inklusive exteriöra derivator) finns att ladda ner här.
///////
The fundamental theorem of calculus and some of its applications:
///////
På svenska: Stokes sats
• Yttre derivata (på Wiktionary)
///////
Sid 45, rad 12: … så många berömda grekiska matematiker: Pythagoras, Euklides, Arkimedes, för att bara nämna de mest kända.
KOMMENTAR: Även Eudoxos bör nämnas här.
/////// Citat:
Eudoxus made important contributions to the theory of proportion, where he made a definition allowing possibly irrational lengths to be compared in a similar way to the method of cross multiplying used today.
The theory developed by Eudoxus is set out in Euclid’s Elements. Definition 4 in that Book is called the Axiom of Eudoxus and was attributed to him by Archimedes.
It is difficult to exaggerate the significance of the theory, for it amounts to a rigorous definition of real number. Number theory was allowed to advance again, after the paralysis imposed on it by the Pythagorean discovery of irrationals.
Another remarkable contribution to mathematics made by Eudoxus was his early work on integration using his method of exhaustion. This work developed directly out of his work on the theory of proportion since he was now able to compare irrational numbers.
/////// Slut citat
KOMMENTAR: Eudoxus, Appolonius från Perga och Arkimedes var enligt min mening de tre största matematikerna från den grekiska antiken. Det vi vet om Pythagoras är endast fragment av berättelser i tredje och fjärde hand.
///////
Sid 46, rad 8 nerifrån: … så vet vi att Arkimedes var en enastående matematiker och att han framförallt bidrog med insikter om volymer och areor.
KOMMENTAR: Sådana insikter var en del av Arkimedes mångdimensionella geni. En annan mycket viktig del var integralkalylen. År 1906 återfanns ett manuskript av Arkimedes – kallat The Method – som en s.k. palimpsest, dvs en skinnhud, där medeltidsmunkarna hade skrapat bort Arkimedes ursprungstext, (i vilken han bl.a. beräknade parabelsegmentets area) och ersatt den med olika bibelcitat.
///////
Sid 60, rad 14 nerifrån: Genom att gå upp och ner längs en smal stig som följer rektanglarnas form kan du räkna ut arean.
KOMMENTAR: Rektanglarna har (oftast) konstant bredd (som minskar mot noll när indelningsfinheten ökar), medan de allt smalare rektanglarnas höjd förändras med ändringen av funktionsvärdet. Det MINSTA funktionsvärdet i ett intervall ger en rektangel vars area är mindre än (eller lika med) motsvarande area under funktionsgrafen i detta intervall och summan av dessa ”under-rektanglar” över hela integrationsområdet kallas en UNDERSUMMA till integralen.
På motsvarande sätt ger en det maximala funktionsvärdet i intervallet en rektangel vars area är större än (eller lika med) motsvarande area under funktionsgrafen i detta intervall och summan av dessa ”över-rektanglar” över hela integrationsområdet kallas en ÖVERSUMMA till integralen.
Integralen existerar om och endast om undersumman och översumman har SAMMA GRÄNSVÄRDE när ”finheten” i intervallindelningen närmar sig noll. Se t.ex. The definite Riemann integral of a function.
///////
Sid 105, rad 4: Newton […] gick över kurvan i ett diagram
KOMMENTAR: Newtons differential och integralkalkyl grundade sig på utveckling i s.k. potensserier, närmare bestämt utveckling i vad som senare kom att kallas Taylorserier eller MacLaurinserier. Newton kom fram till sin metod genom att generalisera binomialsatsen – som handlar om utvecklingen av \, (a + b)^n \, – till icke-heltalskoefficienter, som t.ex. \, (a + b)^{1/2} . Denna process inleddes under ”de magiska åren” 1664-1666 då universitet i Cambridge var stängt på grund av pestens härjningar.
Genom sin potensserieutvecklingsmetodik – av Newton kallad The Method of Fluxions – kunde Newton derivera och integrera vilken serieutvecklingsbar funktion som helst – genom att derivera respektive integrera dess Taylorserie term för term.
Newtons tillvägagångssätt gjorde det svårt för honom att presentera sina resultat inom ramen för den serieutvecklingskalkyl som han kommit fram till dem med hjälp av. Han översatte därför resultaten i sitt banbrytande verk Philosophiae Naturalis – Principia Mathematica (1687) till klassisk geometri ”à la Euklides”, vilket resulterade i en massa sällsamma matematiska samband mellan ellipser, parabler och hyperbler.
Newton ”sopade helt enkelt igen spåren” efter sig, och kunde därför heller inte förmå sig att publicera något som han själv var nöjd med om matematiken bakom ”Principia”.
Leibniz däremot utvecklade en superb notation som i princip ännu används, och när han publicerade sin version av differential- och integralkalkylen år 1684 kom detta som en chock för Newton.
Newton hade beskrivit sin metod i ett manuskript från 1671: The Method of Fluxions and Infinite Series: With Its Application to the Geometry of Curve-lines, men detta publicerades inte förrän 1736, nästan tio år efter Newtons död.
///////