This page is a sub-page of our page on Entropy.
///////
Other relevant sources of information:
• Thermodynamics
• Heat
• Temperature
• First law of thermodynamics
• Energy
• Work (thermodynamic)
• Second law of thermodynamics
• Entropy
///////
What follows is a translation of the first part of The Svedberg’s Arbetets Dekadens
(= The Decadence of Work) from 1915:
The water that drives the turbines in our rivers, the air that sets wind motors and windmills in motion, the coal, the wood and the peat which we burn in the boilers, the bread that we eat, all these disparate entities contain a certain something that is absolutely necessary for all life. This something is called energy or work. If we lift \, 1 \, kilogram one meter higher than it previously was, we have carried out an amount of work, which is usually taken to be a unit of measure and termed \, 1 \, kilogram meter.
The work we have carried out by increasing the height of the kilogram by \, 1 \, meter is not lost. By allowing the kilogram to fall back \, 1 \, meter we regain exactly \, 1 \, kilogram meter. Hence, because of its location, the kilogram thus has the ability to do perform work – it contains energy. Similarly, the water above a waterfall has the ability to carry out work when it descends to a lower level; the water contains work. The energy of the waterfall is taken up by the turbine, which passes it, for example, to an electric generator. The generator sends out an electrical current, which has the ability to drive a motor, that is, to perform work.
The electrical current is thus a carrier of energy, but the generator can also feed an electric stove or a cooking apparatus, and therefore the current can generate heat. The generator delivered the current and the turbine drove the generator which in turn was kept in rotation by the waterfall. Hence the waterfall has generated heat, and therefore mechanical work can be transformed into heat. From heat we can produce steam, by which we can operate a steam engine, that is perform work; Thus, heat can be transformed into work. Heat is therefore a form of energy. Other forms of energy are light, sound, nuclear radiation, etc.
It is a characteristic of the different forms of energy that they all can be converted into one another, and that to a certain quantity of one form there always corresponds a certain definite quantity of every other form. Hence the energy itself is indestructible, only the form varies.
The various forms of energy differ from each other by their different ability to perform work. Mechanical energy can be completely converted into heat, but not vice versa. Each kilogram meter of work produces an amount of heat sufficient to warm up \, 0,023 \, grams of water by \, 100° Centigrade. But the mechanical work we sacrificed in this process cannot be fully recovered from the resulting heat.
Suppose that we have converted \, 100 \, kilogram meters into heat by extracting \, 2.3 \, grams of water from a water reservoir of temperature \, 0° Centigrade and then heated this extracted water to \, 100° Centigrade. If we try to extract mechanical work from this system, it turns out that we are at the most able to produce \, 0.23 \times \frac {100}{373} \times 427 = 26 \, kg m . Meanwhile, an amount of heat equivalent to \, 74 \, kg m has shifted from the higher to the lower temperature and evaded our efforts to convert it into work. Consequently, it is impossible to construct a machine, whose only activities would consist in performing external work while cooling a heat reservoir.
One can also express this law thus: It is not possible to bring water to boil by adding ice cubes to it. In such a crass formulation this law appears ridiculously self-evident, but on closer reflection we find that this “obviousness” is merely an expression of knowledge gained by daily experience. The issue can be clarified as follows. Both the water as the ice cubes contain heat, and the temperature of the latter heat is lower than the temperature of the water. By adding the ice cubes to the water, we are offer the water the opportunity to rob the ice of its heat and thus raise its own temperature to the boiling point. It is not allowed, a priori, to reject such a possibility as unreasonable.
Nothing prevents the heat to flow from the ice to the water, just as it can flow in the opposite direction. Experience teaches us that the latter, but never the former, occurs. This implies a certain awareness, a knowledge that we have acquired by observation, something that goes beyond the obvious. This knowledge can be formulated thus: heat cannot by itself move from a lower to a higher temperature. We shall see below that this fact is the manifestation of a general law of nature which is of ominous importance.
It was mainly investigations dictated by technical interest in the work ability of heat, which led to the discovery of the degeneration of energy. The driving force of fire, known since ancient times and used already by Heron of Alexandria to perform work, had in the first decade of the 1800s become of fundamental importance for industry, thanks mainly to the work of a series of English engineers. The steam engine heralds a new era.
A young French artillery officer, Sadi Carnot, son of the well-known statesman and writer L. N. Carnot from the French Revolution and the Napoleonic era, describes in a pamphlet published in 1824: “Réflexions sur la puissance motrice du feu” the lively hopes that were tied to heat engines, and the major role they played already at that time. “To deprive England of its steam engines would be to deprive it of its coal and iron; it would be to make its sources of wealth dry out, destroying its means to prosperity; it would be to destroy the power of the empire. The loss of its fleet, which it regards as its strongest military defense, would probably be less fatal.”
The theory of the steam engine was still unwritten, “the process that consists in the creation of motion through heat has not been considered from a sufficiently general point of view.” One did not know whether the “driving force of fire” was dependent on the materials with which the heat engine was working, for instance steam or air. Neither was it known whether or not the work ability of heat engines was determined by a natural law grounded in the general nature of phenomena. It was this situation that Carnot set out to investigate.
He notes first that heat engines for their business require a temperature difference: The heat must move from a higher to a lower temperature in order for us to be able to extract work from it. If we imagine that a quantity of steam, taken from a boiler \, A \, at temperature \, t_1 \, , is acting on the piston of a cylinder, then the expansion of the steam can be converted into an amount of work \, w_1 . In this process the steam cools to the temperature \, t_2 . If we then compress the steam and let it into a boiler \, B \, at temperature \, t_2 \, , we need for this effort an amount of work \, w_2 \, which is less than \, w_1 .
The result of these two processes is thus that the steam has cooled from \, t_1 \, to \, t_2 \, and the work \, w_1 - w_2 = w \, has been gained. The original state can be restored by compressing the same amount of steam from the boiler \, B , until the temperature has risen to \, t_1 \, , and then admitting it into \, A \, . This restoration process requires the amount of work \, w .
If we now make the assumption that it would be possible to construct a heat engine, which, within the same range of temperatures, delivered a greater amount of work \, w' \, , then one could with the previous machine, while sacrificing only the amount of work \, w \, , restore the original state, and thus keep as pure profit the amount of work \, w'-w . That this is unreasonable, seemed obvious to Carnot. Such a creation of driving power conflicts with the laws of mechanics as well as with the common laws of physics, he says.
Consequently, the efficiency of a heat engine must be independent of the materials it works with, and a given temperature difference can be utilized to obtain a certain specific quantity of work. This quantity represents a limit, which the designers of heat engines must strive to approach, but which in fact can never be fully achieved.
In Carnot’s time scientists still regarded heat as an indestructible substance and in his pamphlet of 1824, he himself takes this stance. The role of heat in e.g. a steam engine was therefore likely to be about the same as the the role of the water in a water mill, and, like the latter’s performance, would be dependent on the height of fall as well as on the rate of flow of water. In accordance with this model, Carnot found experimentally that the work that can be delivered by the steam engine is determined by the difference of temperature (= the “height-of-fall” of the heat) between the cylinder and the condenser, and by the supplied amount of heat.
Carnot died already in 1832. Among his remaining papers, notes have been found that clearly demonstrate that he soon departed from the mainstream conception of heat as an indestructible substance and that he had achieved a clear insight into the fact that the work of a heat engine is extracted by sacrificing a certain amount of heat, as well as that “the overall driving force is an invariant quantity in nature, a quantity that can neither be created nor destroyed”.
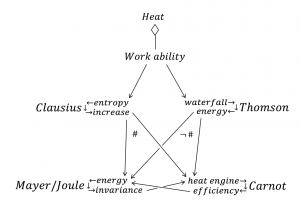
The German physician Mayer and the British brewer and physicist Joule succeeded – some 20 years after the release of Carnot’s pamphlet in 1824 – to convincingly demonstrate that heat can be converted into work and vice versa. From an input of 427 kilogram meter of work was obtained a quantity of heat sufficient to raise the temperature of one kilogram of water \, 1° . According to Mayer and Joule heat must therefore be consumed in the steam engine; according to Carnot’s ideas, the work produced by a heat engine was obtained by an amount of heat that – under temperature reduction – was transferred from the boiler to the condenser. This seemed to imply a contradiction.
The situation was extremely serious, which can be inferred from the fact that leading scientists were seriously discussing the question of whether one might be forced to abandon either Mayer-Joule’s principle of energy invariance or Carnot’s principle of (theoretical) heat engine efficiency. For example, the physicist W. Thomson (later Lord Kelvin) wrote in 1849: “We may seem to be avoiding the difficulty altogether if we would give up Carnot’s fundamental axiom, which is strongly urged by Mr. Joule. But if we would take this approach, we would meet with countless other difficulties.”
The explanation was given shortly after by the German physicist Clausius. Of the heat that is input to a steam engine from the boiler, one part is converted to mechanical work, while another part is transformed from a higher to a lower temperature. Formulated thus, Carnot’s principle is in full compliance with Mayer-Joule’s law of the indestructibility of energy. As Clausius demonstrated, the part of the input heat that is converted into work is related to the amount of heat transferred from the boiler, in the same proportion as the difference of temperature between the boiler and the condenser is related to the temperature of the boiler (measured from absolute zero).
According to Carnot’s principle the theoretical efficiency of a heat engine is independent of the material. Hence it is valid in general that if we input 100 units of heat, we will as a theoretical maximum obtain \, \frac{t_1 - t_2}{t_1 + 273} \times 100 \, units of heat that have been converted into work. The larger the temperature difference, the more work can be extracted.
A machine working within the range of \, 0° - 100° therefore theoretically achieves \, 26% \, work efficiency. If we increase the temperature difference to 3000°, the machine achieves \, 91% \, work efficiency. The sun and the earth together form a heat engine with extremely high efficiency due to the large temperature difference that exists between them. This is why solar radiation is such a “noble” form of energy – it can be almost completely converted into work. The fact that we have not been able to harness this work in any significant way is not the fault of the sun; our own ignorance must be blamed.
The heat as such is of little value for us. Only to the extent that it can be transformed into mechanical work are we able to make use of it. Now since any such conversion is connected with the leveling of a temperature difference, we realize that the “unreacted” amount of heat in the process has decreased its ability to perform work. Since there is no opportunity to give this heat back its lost work ability without the corresponding sacrifice, it follows that our energy supply, our pool of work, is subject to a constant and relentlessly progressing decadence.
In order to enable a more detailed study of this degeneration, Clausius has introduced – as a measure of this degeneration – a mathematically defined term, entropy. If we change a body’s heat content with a small quantity \, Q , its entropy is changed by the value \, Q/T , where \, T \, is the absolute temperature of the body. When heat is transferred from a higher to a lower temperature, its entropy therefore increases and hence its work ability decreases – the work ability degenerates. A system’s entropy cannot be reduced, unless a corresponding increase occurs somewhere within the surrounding environment. Clausius has shown that in all completely reversible processes the entropy remains unchanged. Such processes are e.g. the compression and expansion of a gas as well as the raising and lowering of a weight.
Unfortunately, completely reversible processes do not exist in real life. It is for example not possible to realize a mechanical device that is completely without friction and heat conduction – two inexorably irreversible phenomena. So we are not even able to maintain the entropy in our own world unchanged, it is constantly growing.
At a fleeting glance, occupation with the concept of entropy, work decadence, may seem rather pointless. If such such ineradicable degeneration rules the world – why not pass over this sad fact in silence? Why waste words on something that is hopeless?
A defendant of the study of entropy may argue, that even the love of phenomena as such, as well as the need to get to know their context, force us to seek to penetrate this concept. But the issue also has a practical side. Every piece of knowledge is a means for the improvement of our existence. Maybe then also a detailed knowledge of entropy and the laws by which the decadence of work progresses, can be useful.
We have already won one lesson of significant practical value in the above-referenced formula for the efficiency of heat machines. Without this knowledge the magnificent developments in fuel engines would have been unthinkable, and thus, for example, the inception of air machines. Some branches of electrical engineering originate from a detailed knowledge of entropy, and so do much of physical chemistry and thus many important chemical-technical industries. In fact, the concept of entropy is now so assimilated by the entire physical and chemical research community that it is difficult to find an area where it has not carried out any educational work. Entropy tells us in what direction a process will proceed, as well as whether, under given conditions, an event can even take place or not.
Clausius concept of entropy increase restored compatibility between Mayer/Joule’s concept of energy invariance and Carnot’s concept of heat engine efficiency, the lack of which Thomson was lamenting about.
Functorial and non-functorial relations between energy theories: