This page is a sub-page of the page on our Mathematical Explainatorium.
///////
The sub-pages of this page are:
• Mathematics is Representation
• What is a Mathematician?
• What does it feel like to do Mathematics?
• What is the difference between Mathematics and Science?
• The historical struggle to get rid of meaning
• The Impossibility of Teaching Mathematics
• Mathematical Courtesy
• The Legendary Lusitania
///////
Related pages:
• The Evolution of Geometric Arithmetic
• Math Makers versus Math Fakers
///////
Mathematics is a process driven by Pragma, Awe, and Curiosity:
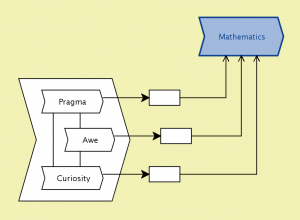
///////
Mathematics driven by Pragma, Awe, and Curiosity – peeking into Create and Apply:
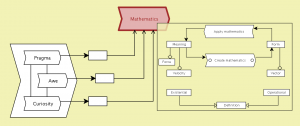
///////
///////
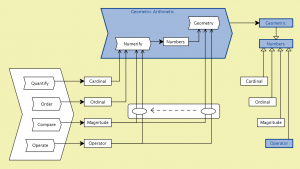
Geometric Numbers – peeking into Numbers:
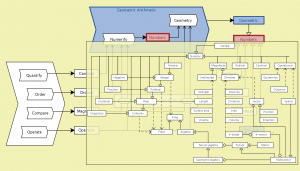
///////
Geometric Numbers – peeking into Operators:
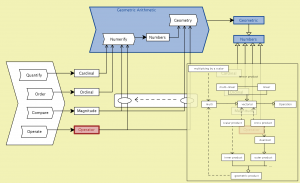
///////
Geometric Numbers – peeking into Geometric:
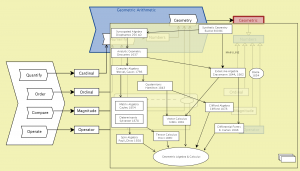
///////
Geometric Numbers – peeking into Geometric Arithmetic:
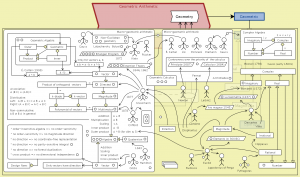
///////
Where do math symbols come from?
John David Walters on TedEd:
///////
What is Mathematics?
Mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true. (Bertrand Russell)
Mathematics – in the sense of the Greeks, began with Thales around 600 BC – as part of an attempt to try to understand the world in a sensible (= non-magical) way. In fact, it was a part of a “scientific awakening” of the human mind against the tyranny of the priests. People started asking questions such as “what is the basic stuff that the universe is made of” – and asking such questions, not to the gods and religious authorities, but to nature itself. This was the birth of the scientific process.
The word ‘mathematics’ is said to go back to Pythagoras (around 500 BC), who called his most advanced disciples ‘mathematikoi’. In the present context, this word will be interpreted in the following way:
Mathematics is the study of the totality of structures that the human mind is able to perceive. Within the language of itself, mathematics can be described as the study of homomorphisms (= structure-preserving transformations) into the mind from its environment – including the mind itself.
\;\; M_{athematics} \, = \, \Hom( \, U_{niverse}, M_{ind} \, ) \,
Life is structure, and since mathematics is the language of structure, it is the language of life, the ultimate ruler of the subspace within which life can be talked and reasoned about.
Hence, mathematics is concerned with the effective and efficient representation of structure. The stronger (= more effective and efficient) the representation, the shorter the computation that has to be performed in order to achieve a certain result. This shortness is referred to by mathematicians as “mathematical elegance.”
///////
Representation and Reconstruction of a Presentant with respect to a Base
Representation: [ \, p_{resentant} \, ]_{B_{ase}} = \left< \, r_{epresentant} \, \right>_{B_{ase}} \,
Reconstruction: \left( \, \left< \, r_{epresentant} \, \right>_{B_{ase}} \, \right)_{B_{ase}} = p_{resentant}
//////////////////////////////////////////////////////////////// På svenska (= in Swedish):
Representation och Rekonstruktion av ett Föremål med hjälp av en Bakgrund
Representation: [ \, f_{öremål} \, ]_{B_{akgrund}} = \left< \, b_{ild} \, \right>_{B_{akgrund}}
Rekonstruktion: \left( \, \left< \, b_{ild} \, \right>_{B_{akgrund}} \, \right)_{B_{akgrund}} = f_{öremål}
Vad är matematik?:
////////////////////////////////////////////////////////////////
The Map of Mathematics (by Domain of Science):
Mathematics: Beauty vs Utility – Numberphile (Discussion with Cédric Villani):
The Fields Medal (with Cédric Villani) – Numberphile:
//////// Mixed languages (English and Swedish) below
Varför kunna matematik? (av Mikael Gustafsson):
Sverige ska bli bäst i matematik (av Wallenbergstiftelserna):
Sweden – Becoming a World Leader in Mathematics (by the Wallenberg Foundations):