This page is a sub-page of our page on Research Areas.
///////
• From Exploratorium to Explainatorium: The story behind our change of name
• Some of our earlier math education projects.
///////
The sub-pages of this page are:
• Mathematical Art Gallery
• Learning Object Repository
• What is Mathematics?
• First Class Mathematics
• Math Book Reviews
• Mathematical Concepts
• Math Bandages
• The Difficultification Industry
• New Paradigms and Tools for Math Education
• Reawakening Interest
///////
Related KMR-pages:
• Mathematics is Representation
• What is a Mathematician?
• What does it feel like to do Mathematics?
• What is the difference between Mathematics and Science?
• The historical struggle to get rid of meaning
• The Impossibility of Teaching Mathematics
• Math Makers versus Math Fakers
• Mathematical Courtesy
///////
Other related sources of information:
• The MathRehab channel on YouTube
• MathTrek – Discovering New Ways of Scientific Thinking.
• Introduction to mathematical thinking
• The Map of Mathematics in the Quanta Magazine
• The Langlands Program: ‘Amazing’ Math Bridge Extended Beyond Fermat’s Last Theorem,
in the Quanta Magazine, 6 April 2020.
• With Category Theory, Mathematics Escapes From Equality,
by Ana Porta, Quanta Magazine
• Does Time Really Flow? New Clues Come From a Century-Old Approach to Math,
in the Quanta Magazine.
• A Path Less Taken to the Peak of The Math World, in the Quanta Magazine.
• The Teaching Gap : Best Ideas from the World’s Teachers for Improving Education in the Classroom, by James W Stigler and James Hiebert, 2009.
• MathRehab
• Situation Mathematics
• A Mathematician’s Lament by Paul Lockhart
• 2018 review of online learning: weak leadership (by Tony Bates)
• The coming calculus MOOC revolution and the end of math research,
by Math Babe, 20 January 2014.
• Politiken hotar Matematiken av Anders Björner et al.,
Svenska Dagbladet, Debatt, 2 sept 2009 (in Swedish).
• What happens when Math goes wrong? with Matt Parker.
• Things to do and see in the fourth dimension with Matt Parker.
In Swedish:
• Sveriges PISA-framgång bygger på falska siffror
• Kravet: Skolverkets chef måste svara riksdagen om PISA-resultat
• Pisa-myglet i skolan är ett svek mot de svagaste
• Anna Ekström begär ny granskning av resultaten
///////
Representation and Reconstruction of a Presentant with respect to a Background
Representation: \, [ \, p_{resentant} \, ]_{B_{ackground}} \, \equiv \, \left< \, r_{epresentant} \, \right>_{B_{ackground}}
Reconstruction: \, \left( \, \left< \, r_{epresentant} \, \right>_{B_{ackground}} \, \right)_{B_{ackground}} \equiv \,\, p_{resentant}
IMPORTANT: Equality only holds if the representation is total.
///////
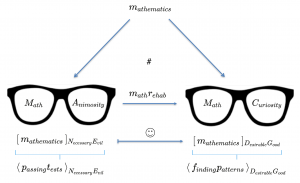
Math Rehab: Changing one’s attitude to mathematics:
Representation: \, [ \, m_{athematics} \, ]_{ \, N_{ecessary} \, E_{vil}} \, \equiv \, \left< \, p_{assing} \, t_{ests} \, \right>_{N_{ecessary} \, E_{vil}}
Representation: \, [ \, m_{athematics} \, ]_{ \, D_{esirable} \, G_{ood}} \, \equiv \, \left< \, e_{xploring} \, p_{atterns} \, \right>_{D_{esirable} \, G_{ood}}
///////
The Mathematical Explainatorium
is a fitting name for my lifetime learning-and-teaching project in mathematics. In fact, it began when I started to teach mathematics at KTH in 1967 (at the age of 19). The opportunity to teach math and the challenges involved in trying to explain it to others – students who, back in the early years, were mostly my own peers – shaped my future teaching career.
During the first two decades I was mostly teaching regular courses, while increasingly trying to add my own personal touch to them – a touch that usually reflected my latest mathematical “love affair” as a graduate student.
My experiences at Ericsson – teaching object-oriented programming techniques between 1989 and 1999 – brought me into the field of modeling, and my engagement with NADA – teaching projective geometry at CVAP in 1984 and being part of developing a prototype called the “Garden of Knowledge” at CID in 1996-97 – led to the formation of the ILE (= Interactive Learning Environment) group at NADA which “morphed” into the KMR (= Knowledge Management Research) group at CSC (formely NADA) in 2001.
Looking back, I can say that during the last two decades I have been been working with some extremely talented people – both within and outside KTH. The KMR group has mainly been involved in projects at the European level, focusing on digital support for learning based on “knowledge pull” and distributed networks of digital (and non-digital) resources. In this work, mathematics has sometimes been used as a kind of testbed, as for example in the projects MathViz and Matriks. The unifying theme has been the “pedagogical elephant in the room” – namely interest.
From necessary evil to desirable good
Question: How can we contribute to diminishing the anxieties that stem from regarding mathematics as a necessary evil?
Answer: By promoting an attitude that regards mathematics more as a desirable good.
Such a shift of attitude would carry with it a change of of mental focus –
from “passing threatening exams” to “finding interesting patterns.”
The attitude of math anxiety is largely based on the fear of not passing tests and hence not beeing “good enough.” A radical approach would be to introduce a global ban on math tests – since they could be seen as a mental counterpart to nuclear tests.
A more pragmatic approach would be to provide new ways to recover from anxiety and rekindle interest. Sadly, a genuine interest in math cannot be established until the fear of math has disappeared, which normally cannot be achieved until the person is out of school and the math tests have disappeared for good.
Consequently, one important action to reduce math anxiety is to reduce the “bleeding” of confidence and self-esteem that results from not passing exams – failures that in themselves reinforce such anxieties. The Math Bandages project is designed to contribute to a stress reduction in such cases.
However, in the longer term, math bandages are not sufficient. One of the things that are needed in order to change the present attitude to math along the lines outlined above is stories that deal with interesting mathematical structures – and that deal with them in ways that are interesting enough to capture attention. This is no small challenge in an increasingly attention-driven economy, where the fights for our eyeballs and our eardrums continually serve to decrease our attention span as well as the cognitive complexity of our thinking.
We believe that such mathematical stories are possible to tell, and we have come across several excellent examples at channels such as YouTube. Some of these are embedded (= pointed to) in this Explainatorium – together with some stories that we have composed within our group.
As is discussed below, a major part of making a mathematical story interesting is to:
• explain the ideas involved (ideally on several levels of complexity).
• connect the dots between them, conceptually, historically, and culturally.
///// TO BE CONTINUED
///////
/////// Stubs:
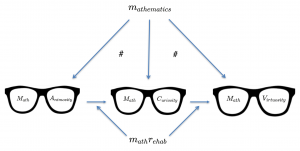
N_{ecessary} \, E_{vil} M_{ath} \, A_{nimosity} D_{esirable} \, G_{ood} M_{ath} \, C_{uriosity} M_{ath} \, V_{irtuosity} M_{ath} \, G_{enerosity} m_{ath} r_{ehab}///////
Problems with today’s math education:
It does not:
• stimulate interest
• promote understanding
• support personalization
• support the transitions between the different school levels
• integrate abstraction and application
• integrate mathematics with human culture
///////
Possibilities of improving math learning:
Promoting life-long learning based on interest by:
using ICT to increase the ”cognitive contact” by:
• visualizing the concepts.
• interacting with the formulas.
• personalizing the presentation.
• routing the questions to live resources.
improving the narrative by:
• showing before proving.
• proving only when the need is evident.
• focusing on the evolutionary history.
Salman Kahn on TED talks: Let’s use video to reinvent education
• The MathRehab channel on YouTube
/////// In Swedish:
Med hjälp av mellanslagstangenten kan man faktiskt köra en “stroboskopliknande” variant av slow motion på YouTube videos. Fördelen är att man kan stanna var som helst och gå vidare till nästa frame när man är redo för detta. Så här gör man:
1. Starta videon.
2. Högerklicka på videon och välj “Loop”.
3. Stanna videon genom att klicka på den.
4. Klicka bort “förslagsfönstret” på nya videos som dyker upp.
5. Starta videon genom att klicka på den.
6. Nu kan man starta och stoppa videon genom att trycka på mellanslagstangenten.
Hastigheten i tryckningarna ger “stroboskopfrekvensen”.
På detta sätt kan man detaljstudera ett dynamiskt förlopp.
/////// Back to English:
Selected publications:
• Naeve, A. (1997), The Garden of Knowledge as a Knowledge Manifold – a Conceptual Framework for Computer Supported Subjective Education, CID-17, TRITA-NA-D9708, Department of Numerical Analysis and Computer Science, KTH, Stockholm.
• Naeve, A. (1999), Conceptual Navigation and Multiple Scale Narration in a Knowledge Manifold, CID-52, TRITA-NA-D9910, Department of Numerical Analysis and Computer Science, KTH, Stockholm.
• Naeve, A. (2001), The Knowledge Manifold – an educational architecture that Supports Inquiry-Based Customizable Forms of E-learning (PDF), Proceedings of the 2nd European Web-based Learning Environments Conference (WBLE 2001), Lund, Sweden, October 24-26, 2001.
• Naeve, A. (2001), The Concept Browser – a new form of Knowledge Management Tool (PDF), Proceedings of the 2 nd European Web-based Learning Environments Conference (WBLE 2001), Lund, Sweden, October 24-26, 2001.
• Blomqvist, U., Handberg, L., Naeve, A. (2003), New Methods for focusing on Students’ Learning Process and Reflection in Higher Education. Proceedings of the 28th IUT (Improving University Teaching) Conference, Växjö, Sweden, June 16-19, 2003.
• Naeve, A. (2001), IT-baserade matematikverktyg på KTH, CID-49, TRITA-NA-D0103, Department of Numerical Analysis and Computer Science, KTH, Stockholm.
• Naeve, A. (2001), The Work of Ambjörn Naeve in the Field of Mathematics Educational Reform (PDF), CID-110, TRITA-NA-D0104, Department of Numerical Analysis and Computer Science, KTH, Stockholm.
• Naeve, A. (2001), Projective Drawing Board – Dynamic Geometric Explorations.
• Naeve, A. (2001), Begreppsmodellering och matematik, CID-109, TRITA-NA-D0103, Department of Numerical Analysis and Computer Science, KTH, Stockholm.
• Taxén, G., Naeve, A. (2001), CyberMath – Exploring Open Issues in VR-based Learning, SIGGRAPH 2001 Educators Program, In SIGGRAPH 2001 Conference Abstracts and Applications, pp. 49-51.
• Taxén, G., Naeve, A., (2001), CyberMath: A Shared Virtual Environment for Mathematics Exploration , Proceedings of the 20:th World Conference on Open Learning and Distance Education (ICDE-2001), Düsseldorf, Germany, April 1-5, 2001, Available on Compact Disc.
• Naeve, A., Nilsson, M. (2004), ICT-enhanced Mathematics Education within the Framework of a Knowledge Manifold, Accepted for presentation at the 10th International Congress of Mathematics Education (ICME), Copenhagen, Denmark, July 4-11, 2004.
• Nilsson, M., Naeve, A. (2004), On designing a global infrastructure for content sharing in mathematics education, Accepted for presentation at the 10:th International Conference on Mathematics Education (ICME), Copenhagen, Denmark, July 4-11, 2004.
///////
Project Math Explainatorium
• Ideology: Within the math explainatorium project we want to emphasize the speculative and creative aspects of mathematics as a way to reconnect with your belief in your ability to think.
• Aim: To stimulate interest in mathematics among young and old by emphasizing “week-end mathematics”.
• Basic idea: Problematize and dramatize the major mathematical concepts by anchoring them in the history of ideas.
• Methdod: Improving the narrative – e.g., by showing without necessarily proving.
• Form: The news of yesterday: Proust: “In Search of Lost Mathematics.” Knowledge components (featuring Pythagoras, Archimedes, Newton, …) are “tied together” by a ”news anchor in space-time” who follows different trails along the evolution of mathematical ideas.
Some concrete examples of story-scripts based on this math-education ideology aiming at raising interest in mathematics can be found on our page about Mathematical Hikes.
///////
Overall ambition of the Math Explainatorium Project:
Aiming to support a transformation from math fakers to math makers by contributing to:
(1) A “smorgasbord” of interest-provoking, First-Class Mathematics
with historical and cultural embeddings.
(2) A collection of Math Bandages that are helpful in passing higher-education exams
in mathematics for science, technology and engineering.
(3) An infrastructure that enables and promotes the evolution of
PeopleSMART learning environments within the STEM field.
///////
Strategic Parts of the Math Explainatorium web site
• What is Mathematics?
• Mathematics is Representation
• What does it feel like to do Mathematics?
• Mathematical Courtesy
• The Historical Struggle To Get Rid Of Meaning
• The Impossibility Of Teaching Mathematics
• Some Traditional Patterns Of Math Education
• Mathematical Concepts
• New Paradigms and Tools for Math Education
• Reawakeing Interest in Mathematics
• Exploring and Explaining
///////
Mainstream Traditional Parts of the Math Explainatorium Learning Object Repository:
Algebra:
• Linear Algebra
• Matrix Algebra
• Some Basic Algebraic Concepts
Calculus:
• Calculus of One Real Variable
• Calculus of Several Real Variables
• Calculus of One Complex Variable
Non-Mainstream Traditional Parts (of the Math Explainatorium Learning Object Repository):
Algebra:
Geometry and Algebra:
• Geometric Algebra
• Clifford Algebra
Geometry and Calculus:
Geometry:
• Plane Curves
• Surfaces
• Triangles
• Metric Geometry
• Affine Geometry
• Projective Geometry
///////
Non-Traditional Parts (of the Math Explainatorium Learning Object Repository):
Algebra:
• Business Algebra
• Knowledge Algebra
• Social Algebra
• Discourse Algebra
Calculus:
Geometry:
• The Evolution of Geometric Arithmetic
Category Theory:
Short-Cirquiting Learning Objects:
• Numbers
• Music
• Art
• Stories
• Vectors
• Shift of Basis
• Interactive Learning Objects
///////