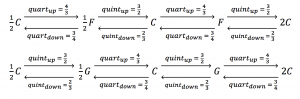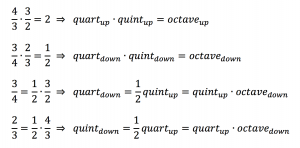This page is a sub-page of our page on Music.
///////
Related KMR pages:
• Solfege: An Abstract Key System
• Instantiations of Solfege in different Keys
• Abstract and Concrete Chord Circles
• Generating the Quint Circle from the Mathematical Cogwheels
• Chord Ladder
• Transposition of Key = Shift of Basis in Music
///////
Other related sources of information:
• …
///////
Some tunes that make use of only quarts and quints
• Johnny B. Goode {C, F, G}, (Chuck Berry)
• Sweet Little Sixteen {E, A, B}, Chuck Berry
• Sweet Little Sixteen {E, A, B}, The Rolling Stones
• Sweet Little Sixteen {E, A, B}, John Lennon
• I Saw Her Standing There {E, A, B} & Twist And Shout {C, F, G},
Paul McCartney & Bruce Springsteen
///////
\, q_{uart} \cdot q_{uint} = o_{ctave} \, .
\, f_a \cdot s_o = 2^{\, \frac{5}{12}} \cdot 2^{ \, \frac{7}{12}} = 2^{\, (\frac{5}{12} + \frac{7}{12})} = 2^{\, \frac{12}{12}} = 2^{\, 1} = 2 \, d_o .
///////
Solfege (= key-independent) interaction schema of Quarts and Quints:
The Solfege interaction schema of Quarts and Quints instantiated in the key of C:
Up-Down frequency-based relationships for both Quarts and Quints:
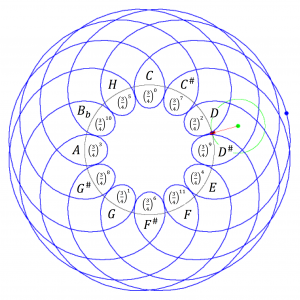
A slideshow comparing the up- and down motions of the quarts:
The resulting patterns are symmetric, because:
On a 12 half-tones scale we have
\, +5n = +6n - n \, (mod \, 12) \, and
\, -5n = -6n + n = +6n + n \, (mod \, 12) ,
and the points
\, +6n - n \, (mod \, 12) \, and
\, +6n + n \, (mod \, 12) \,
are symmetrically placed
in relation to the line connecting the points
\, 6(2n) = 0 \, (mod \, 12) \, and
\, 6(2n+1) = 6 \, (mod \, 12) .
A slideshow comparing the up- and down motions of the quints:
The resulting patterns are symmetric, because:
On a 12 half-tones scale we have
\, +7n = +6n + n \, (mod \, 12) \, and
\, -7n = -6n -n = +6n -n \, (mod \, 12) ,
and the points
\, +6n + n \, (mod \, 12) \, and
\, +6n - n \, (mod \, 12) \,
are symmetrically placed
in relation to the line connecting the points
\, 6(2n) = 0 \, (mod \, 12) \, and
\, 6(2n+1) = 6 \, (mod \, 12) .
Frequency-based relationships between Quarts and Quints:
A slideshow comparing the up-motion of the Quints
and the down motion of the Quarts:
The resulting patterns are identical, because:
On a 12 half-tones scale we have
\, +7n = -5n \, (mod \, 12) \, for all n \in N ,
which in frequency-based terms translates to
\, (\frac{3}{2})^n = (\frac{3}{4})^n \,(mod \, 2)\, for all n \in N .
A slideshow comparing the up-motion of the Quarts
and the down motion of the Quints:
The resulting patterns are identical, because:
On a 12 half-tones scale we have
\, +5n = -7n \, (mod \, 12) \, for all n \in N \, ,
which in frequency-based terms translates to
\, (\frac{4}{3})^n = (\frac{2}{3})^n \,(mod \, 2)\, for all n \in N .
A slideshow comparing the up-motion of the Quints
and the up-motion of the Quarts:
A slideshow comparing the down-motion of the Quarts
and the down-motion of the Quints:
A slideshow illustrating the frequencies of the Quart-down motion:
///////