This page is a sub-page of our page on Geometric Numbers in Euclidean 3D-space.
///////
Related KMR-pages:
• Clifford Algebra
• Geometric Algebra
• Complex Numbers
///////
Other relevant sources of information:
• Quaternion (at Wikipedia)
• Rotor (at Wikipedia)
• Versor (at Wikipedia)
///////
The quaternions represented as the even subalgebra
of the Clifford algebra \, C_l(e_1, e_2, e_3) \, over the real numbers \, \mathbb {R} .
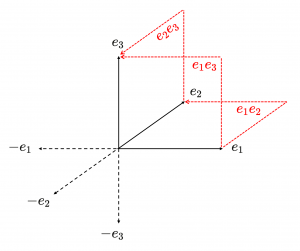
This diagram shows the 1-blades (unbroken black arrows) and the 2-blades (red, dotted, broken arrows) among the blades in the canonical basis for \, C_l(e_1, e_2, e_3) .
The negatives of the 1-blades are shown as dotted black arrows.
The 2-blades \, \textcolor {red} {e_1 e_2} \textcolor {black} {,} \textcolor {red} {e_2 e_3} \textcolor {black} {,} \textcolor {red} {e_1 e_3} \,
represent the directed area within the corresponding squares.
Hence we have for \, k \neq i \, : \, (e_i e_k)^2 = e_i e_k e_i e_k = - e_k e_i e_i e_k = - e_k e_k = -1
Addition rule for the even subalgebra of \, C_l(e_1, e_2, e_3) \, :
\, (\alpha \textcolor {red} 1 + \alpha_{12} \textcolor {red} {e_1 e_2} + \alpha_{23} \textcolor {red} {e_2 e_3} \, + \alpha_{13} \textcolor {red} {e_1 e_3}) \, +
\, + \, (\alpha' \textcolor {red} 1 +\alpha'_{12} \textcolor {red} {e_1 e_2} + \alpha'_{23} \textcolor {red} {e_2 e_3} + \alpha'_{13} \textcolor {red} {e_1 e_3}) \stackrel {\mathrm{def}}{=} \,
\stackrel {\mathrm{def}}{=} \, (\alpha + \alpha') \textcolor {red} 1 + (\alpha_{12} + \alpha'_{12}) \textcolor {red} {e_1 e_2} + (\alpha_{23} + \alpha'_{23}) \textcolor {red} {e_2 e_3} + (\alpha_{13} + \alpha'_{13}) \textcolor {red} {e_1 e_3} .
Multiplication table for the even subalgebra of \, C_l(e_1, e_2, e_3) \, :
\, \begin{matrix} * & ~ & \textcolor {red} 1 & \textcolor {red} {e_1 e_2} & \textcolor {red} {e_2 e_3} & \textcolor {red} {e_1 e_3} \\ & & & & & & \\ \textcolor {red} 1 & ~ & \textcolor {red} 1 & \textcolor {red} {e_1 e_2} & \textcolor {red} {e_2 e_3} & \textcolor {red} {e_1 e_3} \\ \textcolor {red} {e_1 e_2} & ~ & \textcolor {red} {e_1 e_2} & - \textcolor {red} 1 & \textcolor {red} {e_1 e_3} & - \textcolor {red} {e_2 e_3} \\ \textcolor {red} {e_2 e_3} & ~ & \textcolor {red} {e_2 e_3} & - \textcolor {red} {e_1 e_3} & - \textcolor {red} 1 & \textcolor {red} {e_1 e_2} \\ \textcolor {red} {e_1 e_3} & ~ & \textcolor {red} {e_1 e_3} & \textcolor {red} {e_2 e_3} & - \textcolor {red} {e_1 e_2} & - \textcolor {red} 1 \, \end{matrix} \, .
Multiplication table for the quaternions:
\, \begin{matrix} * & ~ & \bold 1 & \;\; \bold i & \, \bold j & \, \bold k \\ & & & & & & \\ \bold 1 & ~ & \bold 1 & \;\; \bold i & \;\; \bold j & \;\; \bold k \\ \bold i & ~ & \bold i & - \bold 1 & \;\; \bold k & - \bold j \\ \bold j & ~ & \bold j & - \bold k & - \bold 1 & \;\; \bold i \\ \bold k & ~ & \bold k & \;\; \bold j & - \bold i & - \bold 1 \, \end{matrix} \, .
///////
Substituting \, \bold 1 = \textcolor {red} {1} \, , \, \bold i = \textcolor {red} {e_1 e_2} \, , \, \bold j = \textcolor {red} {e_2 e_3} \, , \bold k = \textcolor {red} {e_1 e_3} \, and comparing the two addition tables and the two multiplication tables, we see that the respective tables are identical, and therefore they represent the same mathematical structure, or, as a mathematician would say, they are isomorphic.
///////
What are quaternions, and how do you visualize them? A story of four dimensions.
(3Blue1Brown on YouTube):
///////
Quaternions Explained Briefly (Mathoma on YouTube):
///////
Understanding Quaternions through Geometric Algebra (Jorge Rodriguez on YouTube):
///////