This page is a sub-page of our page on Functions with special properties
///////
The sub-pages of this page are:
• …
///////
Related KMR-pages:
• …
///////
Books:
• Differential and Integral Calculus by Richard Courant.
///////
Other relevant sources of information:
• …
///////
Anchors into the text below:
• Topology
///////
Continuity
/////// Quoting Courant: Differential and Integral Calculus, Vol. I, p. 463:
As in the case of functions of one variable, the basic requirement that functions should be capable of being represented geometrically leads to analytic conditions of continuity. Here again, the concept of continuity is given by the following definition:
A function \, z = f(x, y) , defined in a region \, R , is said to be continuous at the point \, (a, b) \, of \, R \, if for all points \, (x, y) \, near \, (a, b) \, the value of the function \, f(x, y) \, differs but little from \, f(a, b) , the difference being arbitrarily small if only \, (x, y) \, is near enough to \, (a, b) .
More precisely: the function \, f(x, y) , defined in a region \, R , is continuous at the point \, (a, b) \, of \, R , provided that for every positive number \, \epsilon \, it is possible to find a positive distance \, \delta = \delta(\epsilon) \, – in general depending on \, \epsilon \, and tending to \, 0 \, with \, \epsilon \, – such that for all points of the region whose distance from \, (a, b) \, is less than \, \delta , that is, for which the inequality \, (x-a)^2 + (y-b)^2 ≤ {\delta}^2 \, holds, the relation \, | f(x, y) - f(a, b) | ≤ \epsilon \, is satisfied.
Or, in other words, the relation \, | f(a+h, b+k) - f(a, b) | ≤ \epsilon \, is to hold for all pairs of values \, (h, k) \, such that \, h^2 + k^2 ≤ {\delta}^2 \, and \, (a+h, b+k) \, belongs to the region \, R .
If a function is continuous at every point of a region \, R , we say that it is continuous in \, R .
In the definition of continuity we can replace the distance condition \, h^2 + k^2 ≤ {\delta}^2 \,
by the following equivalent condition:
To every \, \epsilon > 0 \, there shall correspond two positive numbers \, {\delta}_1 \, and \, {\delta}_2 \, such that \, | f(a+h, b+k) - f(a, b) | ≤ \epsilon \, whenever \, | h | ≤ {\delta}_1 \, and \, | k | ≤ {\delta}_2 .
The two conditions are equivalent. For if the original condition is fulfilled, so is the second if we take \, {\delta}_1 = {\delta}_2 = \delta / \sqrt{2} ; and conversely, if the second condition is fulfilled so is the first, if for \, \delta we take the smallest of the two numbers \, {\delta}_1 \, and \, {\delta}_2 .
The following facts are almost obvious:
The sum, difference, and product of continuous functions are also continuous. The quotient of continuous functions is continuous except where the denominator vanishes. Continuous functions of continuous functions are themselves continuous. In particular, all polynomial functions are continuous, and all rational fractional functions are also continuous except where the denominator vanishes.
Discontinuities
In the case of functions of one variable we met with three kinds of discontinuities: infinite discontinuities, jump discontinuities, and discontinuities at which no limit is approached from one side or both. With functions of two or more variables no such simple classification is possible. In particular, the situation is made more complicated by the fact that discontinuities may occur not merely at isolated points but also along whole curves.
Thus for the function \, z = \frac{1}{x-y} \, the line \, x = y \, is a line of infinite discontinuity. As we approach this line from one side or the other the values of \, z \, increase numerically beyond all bounds through positive or through negative values.
The function \, z = \frac{1}{{(x-y)}^2} \, has the same line of discontinuity but tends to \, + \infty \, as we approach the line from either side.
The interactive simulation that created the two movies above.
The function \, z = \frac{1}{x^2+y^2} \, has the single point of discontinuity at \, (x, y) = (0, 0) .
The function \, z = \sin \frac{1}{\sqrt{x^2 + y^2}} \, tends to no limit as we approach the origin.
The surface that it represents is obtained by rotating the graph of the function \, y = \sin \frac{1}{x} \, about the \, y -axis.
/////// End of quote from Courant: Differential and Integral Calculus
///////
A prequel to differentiation
Functions of one real variable:
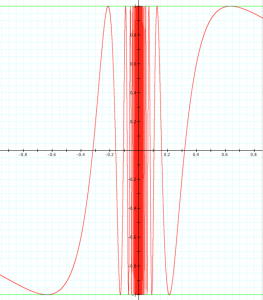
\, y = \sin \frac{1}{x} \, is discontinuous at the point \, x = 0 .
///
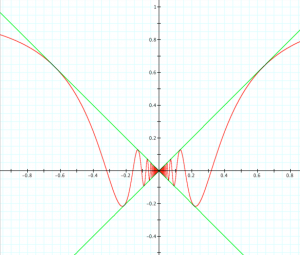
\, y = x \sin \frac{1}{x} \, is continuous but not differentiable at the point \, x = 0 .
///
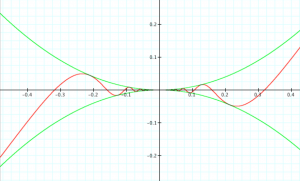
\, y = x^2 \sin \frac{1}{x} \, is differentiable once but not twice at the point \, x = 0 .
///
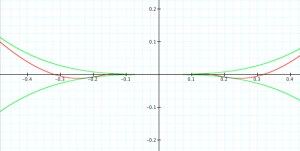
\, y = x^3 \sin \frac{1}{x} \, is differentiable twice but not three times at the point \, x = 0 .
The interactive simulation that created the four pictures above.
///
Functions of two real variables:
Substituting \, \sqrt{x^2 + y^2} \, instead of \, x \, above is geometrically equivalent to rotating the functions \, y = f(x) \, depicted above around the vertical axis. This produces the 3D analogy \, z = f(x, y) \, :
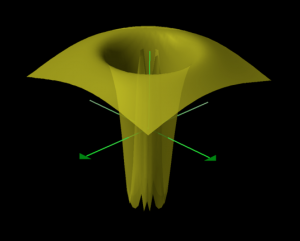
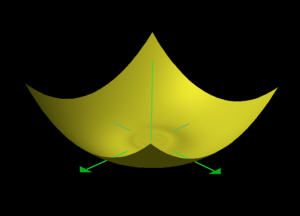
\, z = \sin \frac{1}{\sqrt{x^2 + y^2}} \, is not continuous at the point \, (x, y) = (0, 0) .
///
\, z = \sqrt{x^2 + y^2} \sin \frac{1}{\sqrt{x^2 + y^2}} \, is continuous but not differentiable
at the point \, (x, y) = (0, 0) .
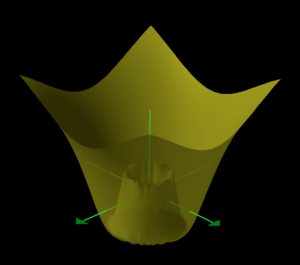
///
\, z = (x^2 + y^2) \sin \frac{1}{\sqrt{x^2 + y^2}} \, is differentiable once but not twice
at the point \, (x, y) = (0, 0) .
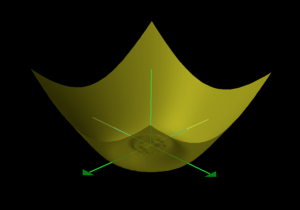
///
\, z = {(x^2 + y^2)}^{ \frac{3}{2}} \sin \frac{1}{\sqrt{x^2 + y^2}} \, is differentiable twice but not three times
at the point \, (x, y) = (0, 0) .
The interactive simulation that created the four pictures above.
///////
A “spiky” function z = f(x, y) that is continuous – even at the origin
\, z = x \sin \frac{1}{y} + y \sin \frac{1}{x} \, if \, | x y | > 0 , and \, z = 0 \, if \, | x y | = 0 .
The interactive simulation that created this movie
///////
An example of a non-eliminable discontinuity for a function of two variables:
\, z = \dfrac{xy}{x^2+y^2} \, : \, {\mathbb{R}}^2 \rightarrow \mathbb{R} .
The interactive simulation that created these two movies
/////// Quoting Courant: Differential and Integral Calculus, Vol. II, p. 464:
Another instructive example of a discontinuous function is given by the rational function
\, z = \dfrac{xy}{x^2+y^2} \, : \, {\mathbb{R}}^2 \rightarrow \mathbb{R} .
In the first instance the function is undefined at the point \, (x, y) = (0, 0) , and we supplement the definition by assuming that \, z(0, 0) = 0 . This function has a peculiar type of discontinuity at the origin. If we put \, x = 0 , that is, if we move along the \, y -axis, the function becomes \, z(0, y) = 0 , which has the constant value \, 0 \, for all values of \, y . Along the \, x -axis we likewise have \, z(x, 0) = 0 .
Nevertheless, the function \, z(x, y) \, is discontinuous when considered as a function of the two variables \, x \, and \, y . For at every point of the line \, y = x \, (in the plane \, z = 0 ) we find that \, z = \frac{1}{2} , so that arbitrarily near the origin we can find points at which \, z \, assumes the value \, \frac{1}{2} . The function is therefore discontinuous at the origin, and cannot be defined at the origin in such a way as to make it continuous.
The above example shows that a function can be continuous in \, x \, for every fixed value of \, y \, and continuous in \, y \, for every fixed value of \, x \, and yet discontinuous when considered as a function of the two variables. The essential point in the definition of continuity is that the value of the function at a point \, P \, must be arbitrarily close to the value of the function at a point \, Q \, , provided only that \, Q \, is near enough to \, P \, ; it is not permissible to restrict the position of \, Q \, relative to \, P \, in any other way.
/////// End of quote from Courant: Differential and Integral Calculus
\, z = \dfrac{xy}{x^2+y^2} \, : \, {\mathbb{R}}^2 \rightarrow \mathbb{R} .
The interactive simulation that created these two movies
///////
Open Sets in one dimension and several dimensions
• Open set
Topology
/////// Quoting Wikipedia (on Topology):
In mathematics, topology (from the Greek words τόπος, ‘place, location’, and λόγος, ‘study’) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself.
/////// End of Quote from Wikipedia.
Topological Space
/////// Quoting Wikipedia (on Topological space):
A topological space is a set endowed with a structure, called a topology, which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity.
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but, generally, cannot be measured by a numeric distance. More specifically, a topological space is a set of points, along with a set of neighbourhoods for each point, satisfying a set of axioms relating points and neighbourhoods.
Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopies. A property that is invariant under such deformations is a topological property. Basic examples of topological properties are: the dimension, which allows distinguishing between a line and a surface; compactness, which allows distinguishing between a line and a circle; connectedness, which allows distinguishing a circle from two non-intersecting circles.
///////
Definition of a topology:
• via open sets.
• via neighborhoods.
/////// End of Quote from Wikipedia.
• Topology
• Topological space
Topology versus “a topology” (PBS on YouTube):
NOTE: There is a similar difference between ‘algebra’ versus ‘an algebra’.
///////
Functions with special properties at the origin:
• The Peano surface
///////