This page is a sub-page of our page on Calculus of Several Real Variables.
///////
Related KMR-pages:
• Directional Derivative
• Vector Analysis
In Swedish:
///////
Other relevant sources of information:
• Gradient
• Contour line
///////
The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.
///////
Other relevant sources of information:
• Gradient
• Contour line
///////
The interactive simulations on this page can be navigated with the Free Viewer
of the Graphing Calculator.
///////
https://kmr.dialectica.se/wp/research/math-rehab/learning-object-repository/calculus/calculus-of-several-real-variables/gradients/Gradients/
///////
Anchors into the text below:
https://kmr.dialectica.se/wp/research/math-rehab/learning-object-repository/calculus/calculus-of-several-real-variables/gradients/Gradients/
• Gradients
• Gradients of flying carpets and level surfaces
///////
Preliminaries:
Let E_2 = [ {\textbf{e}}_x, {\textbf{e}}_y ] be an orthonormal basis for \mathbb{R}^2 , and let E_1 = [ \textbf{e} ] be an orthonormal basis for \mathbb{R}^1 . Moreover, let the position vector \textbf{r} in \mathbb{R}^2 be expressed as a linear combination of the basis vectors of E_2 :
\textbf{r} \equiv r_x {\textbf{e}}_x + r_y {\textbf{e}}_y \, .
The vectors r_x {\textbf{e}}_x and r_y {\textbf{e}}_y are called the components of the vector \textbf{r} , and the sequence of coefficients (r_x, r_y) are called the coordinates of the vector \textbf{r} relative to the basis E_2 .
IMPORTANT: The above Wikipedia article on the concept of basis mistakenly equates the concepts of components and coordinates (probably because there is an isomorphism between them in the most common cases). This mistake is at the root of a fundamental confusion that, for example, makes it difficult to understand the coordinate-free nature of geometric algebra. Computations in geometric algebra (almost) always make use of components and (always) never make use of coordinates.
In mathematics and physics, a component is a vector, but a coordinate is a scalar.
////////
Dual basis = cobasis = reciprocal basis: (based on Wikipedia)
To perform operations with a vector, we must have a straightforward method of calculating its coordinates (by Wikipedia erroneously equated with its components). In a Cartesian frame, the necessary operation is the dot product of the vector and the corresponding basis vector.
\textbf{x} \equiv x_1 {\textbf{e}}_1 + x_2 {\textbf{e}}_2 + x_3 {\textbf{e}}_3 \equiv (\textbf{x} \cdot \textbf{e}_1) \textbf{e}_1 + (\textbf{x} \cdot \textbf{e}_2) \textbf{e}_2 + (\textbf{x} \cdot \textbf{e}_3) \textbf{e}_3,
where \textbf{e}_k are the basis vectors of the frame. The coordinates of \textbf{x} have been found by:
x_k = \textbf{x} \cdot \textbf{e}_k .
IMPORTANT: The the above is true if and only if the vectors of the Cartesian frame form an orthonormal basis.
In a non-Cartesian frame, we do not necessarily have \textbf{e}_i \cdot \textbf{e}_j = 0 for all i \neq j . However, it is always possible to find a vector \textbf{e}^i such that x^i = \textbf{x} \cdot \textbf{e}^i , (i = 1, 2, 3)
In fact, the equality holds when \textbf{e}^i is the dual basis of \textbf{e}_i (see below). Notice the difference in position of the index i .
In an orthonormal frame we have \textbf{e}^i = \textbf{e}_i . The concept of dual basis is further discussed below.
The coordinates of a function f :
In the bases E_2 for its domain and E_1 for its codomain,
a function f from \mathbb{R}^2 to \, \mathbb{R} \, can be described by {{\mathbb{R}^2 \, \stackrel {f} {\longrightarrow} \, \mathbb{R} \:}\atop {\: (x,y) \, \longmapsto \, f(x,y) } } {\,} .
The coordinates of the differential of the function f :
The differential df of the function f at the point (a,b) \in \mathbb{R}^2 is given by:
df_{(a,b)} = \frac{\partial f}{\partial x}_{(a,b)} dx + \frac{\partial f}{\partial y}_{(a,b)} dy. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \, (1.1)
The equation of a level curve of the function f :
The equation of the level curve ( \, f = c_{onstant} \, ) of the function f
through the point (a,b) is given by:
f(x,y) = f(a,b). \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \qquad \qquad \quad \;\, (1.2)
The equation of the tangent line to a level curve of the function f :
The equation of the tangent to the level curve of the function f at the point (a,b)
is given by:
\, \frac{\partial f}{\partial x}_{(a,b)} (x-a) + \frac{\partial f}{\partial y}_{(a,b)} (y-b) = 0. \qquad \qquad \qquad \qquad \qquad \qquad \;\;\;\, (1.3)
Gradients and gradient vectors :
The gradient of the function f :
The gradient of the function f : \, \mathbb{R}^2 {\; \longrightarrow} \; \mathbb{R} is the function {\nabla f} : \, \mathbb{R}^2 {\; \longrightarrow} \; \mathbb{R}^2
defined by:
{{\mathbb{R}^2 \, \stackrel {\; \nabla f} {\; \longrightarrow} \;\;\;\; \mathbb{R}^2 \:}\atop \;\; (a,b) \, \longmapsto \; {\; \nabla f}_{(a,b)} } . \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \qquad \qquad \qquad \; (1.4)
Hence the value of {\nabla f} at the point (a, b) is {\nabla f}_{(a,b)} , pronounced “the gradient of f at the point (a, b) “.
////// Introduce the term vector field.
TERMINOLOGY: We will talk about a gradient field when we refer to the entire vector field of a gradient, and we will talk about a gradient vector when we refer to a single vector from a gradient field.
The coordinates of the gradient field and a gradient vector of the function f :
The coordinates of the gradient field {\nabla f} of the function f
in the basis E_2 = [ {\textbf{e}}_x, {\textbf{e}}_y ] for \mathbb{R}^2 are given by:
{\nabla f}(x, y) = (\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y}). \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \qquad \qquad (1.5)
The coordinates of the gradient vector {\nabla f}(x,y) of the function f at the point (a, b) in the basis E_2 = [ {\textbf{e}}_x, {\textbf{e}}_y ] for \mathbb{R}^2 are given by:
{{ \mathbb{R}^2 \, \stackrel {\; \nabla f(x,y)} {\; \longrightarrow} \;\; \mathbb{R}^2 \:}\atop {\;\;\; (a,b) \, \longmapsto \; (\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y})_{(a,b)} } } {\,}, \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \;\; (1.6)
which means that:
{\nabla f}(x,y)_{(a, b)} = (\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y})_{(a, b)}. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (1.6′)
////// FORTS:
Theorem: the gradient vector {\nabla f}(x, y)_{(a, b)} of the function f(x,y) at the point (a,b) is perpendicular to the tangent to the level curve of the function f(x,y)
at the point (a,b) .
Proof: This follows directly from formula (1.3) above.
//////////
Gradient vectors of flying carpets and their corresponding level surfaces :
The “flying carpet” style equation for the graph of the function f can be expressed as:
z = f(x, y). \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \, (1.7)
Define g(x,y,z) \stackrel {\mathrm{def}}{=} f(x,y) - z . Then the zero-level surface for the graph of the function z = f(x, y) can be expressed as:
g(x,y,z) = 0. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \;\;\;\; (1.8)
In the animation below, the “input” function f(x, y) is given by:
f(x, y) = \frac{1}{4} (x^2 + 4 y^2) .
IMPORTANT: The 3D-gradient of the level surfaces \, g(x, y, z) = c_{onstant} \, projects (along the \, z -direction) onto the 2D-gradient of the level curves \, f(x, y) = c_{onstant} \, :
The interactive simulation that created this movie (Explained in English).
The interactive simulation that created this movie (Explained in Swedish).
///////
Gradient of a level surface – example 1:
\, g(x, y, z) = \frac{1}{3} (x^2 + 4 y^2 + 9 z^2) \, .
The interactive simulation that created this movie (Explained in English).
The interactive simulation that created this movie (Explained in Swedish).
///////
Gradient of a level surface – example 2:
\, g(x, y, z) = \dfrac{x^2}{A} + \dfrac{y^2}{B} + \dfrac{z^2}{C} \; , \; C < B < A. \, (1.11)
The interactive simulation that created this movie (Explained in English).
The interactive simulation that created this movie (Explained in Swedish).
/////// Translated from Folke Eriksson, Flerdimensionell analys, p.98
The gradient as a covariant vector:
So far we have been working within a single, fixed cartesian coordinate system in \mathbb{R}^n , e.g., the xy-system in \mathbb{R}^2 . In this system we have defined \nabla f = (f'_x, f'_y) . However, the gradient can also be expressed in other coordinate systems that are not necessarily cartesian. For example, if (r, \theta) are polar coordinates, the partial derivatives of the function (r, \theta) \rightarrow f(r \cos \theta, r \sin \theta) = z , that is \frac {\partial z} {\partial r} and \frac {\partial z} {\partial \theta} , can be thought of as coordinates of \nabla f in the r \theta-system. In this case the vector \nabla f itself is one and the same, but it has different coordinates in different coordinate systems.
Without making use of any specific coordinate system it would be possible (according to 3.6 and 3.5) to define the gradient geometrically by making use of the normals of the level curves (respectively the level surfaces), or by using the direction of quickest ascent/descent of the value of the underlying function (as well as a measure of the function’s rate of growth along this direction).
Hence, the gradient gives a more general expression for the changes of a function \, f \, in the neighborhood of a point \, \mathbf {a} \, than that of its partial derivatives, which are only related to a specific coordinate system. In contrast, the gradient contains (albeit implicitly) information about the values of the partial derivatives of a function in all possible coordinate systems.
NOTE: There is an important difference between a gradient vector \, \nabla f \, and a directed segment \, AB , i.e., a vector \, \mathbf {v} . While |\mathbf {v}| (i.e., the length of the segment \, AB \, ) has dimension length, the modulus of the gradient, \, |\nabla f| , has dimension \, \text {length}^{-1} \, (if the values of the function \, f \, are dimension-less quantities). Therefore, in this case, the modulus of the gradient gives the rate of change of the value of the function \, f , i.e., the change of the function’s value per unit of length (as we have seen in section 3.5).
This is related to the fact that under a coordinate transformation the gradient \, \nabla f \, behaves differently from how directed segments behave. For example, if one changes from an orthonormal coordinate system basis vectors \, { \mathbf {e}}_i \, to a coordinate system with basis vectors \, 2 {\mathbf{e}}_i , we have for a directed segment:
\mathbf {v} = \sum\limits_i v_i {\mathbf {e}}_i = \sum\limits_i \frac {1}{2} v_i (2 {\mathbf{e}}_i) = \sum\limits_i v'_i \, (2 {\mathbf{e}}_i) ,
which means that we have \, v'_i = \frac{1}{2} v_i . Moreover, since \, x_i = 2 x'_i , it follows from the chain rule that the coordinates of the gradient in the new system are given by:
\dfrac{\partial f}{\partial x'_i} = \sum\limits_k \dfrac{\partial f}{\partial x_k} \dfrac {\partial x_k}{\partial x'_i} = \sum\limits_i \dfrac {\partial f}{\partial x_i} \dfrac {\partial x_i}{\partial x'_i} = 2 \dfrac {\partial f}{\partial x_i} .
Therefore, it is unnecessarily limiting to write e.g., \, \nabla f = \sum \frac {\partial f}{\partial x_i} {\mathbf{e}}_i .
It is much more general to introduce the scalar product \, \nabla f \cdot \mathbf{v} , since the formula \, \nabla f \cdot \mathbf{v} = \sum \frac {\partial f}{\partial x_i} \, v_i \, for such a scalar product is valid in every coordinate system.
In contrast, the formula \, \mathbf{v} \cdot \mathbf{u} = \sum v_i u_i \, for two directed segments is only valid in orthonormal coordinate systems. In our example above of a coordinate transformation we have \, \frac {\partial f}{\partial x_i} \, v_i = \sum \frac {\partial f}{\partial x'_i} \, v'_i , which is unchanged (= invariant) under the transformation, but \, \sum {v_i}^2 = 4 \sum {v'_i}^2 , which is not invariant since we are changing into a non-orthonormal coordinate system.
For reasons that will appear later, it is appropriate to write \, \nabla f \, as a matrix \, G \, with one row, and a directed segment \, \mathbf {v} \, , i.e., a vector, as a matrix \, V \, with one column. Then the scalar product \, \nabla f \cdot \mathbf{v} \, can be identified with the matrix product \, GV .
In applications to physics (and other areas) there are many entities that behave as vectors of one kind or the other during coordinate transformations; entities that also have other physical dimensions.
Some entities, as for example velocity, have dimension length/time and are transformed in the same way as directed segments. Such entities are called contravariant vectors.
Other entities, such as for example force (which is often the gradient of a function) are transformed in the same way as gradients. Such entities are called covariant vectors.
As long as one only transforms between orthonormal coordinate systems one can compute in the same way with both contravariant and covariant vectors, but when one involves a non-orthonormal coordinate system in the transformation, the different kinds of vectors must be treated differently.
In a non-orthonormal coordinate system it is not in general easy to define coordinates for directed segments in a suitable manner, because one needs to compute with different basis vectors at different points of the segment.
For example, in polar coordinates (with basis vectors \, {\mathbf{e}}_r \, respectively \, {\mathbf{e}}_{\theta} \, ) one needs to compute with the directions that the lines \, \theta = {\theta}_0 \, respectively the circles \, r = r_0 \, have at different points. In such cases the basis vectors may in general be different at different points of a segment \, AB .
In the general case it is better to make use of the chain rule, which gives the transformation formulas for the coordinates of a gradient (cf (4), page 84).
By definition, the coordinates of a covariant vector \, \mathbf{v} \, is an \, n-tuple of numbers \, u_k (S), k = 1, 2, \dots, n \, , which varies with the coordinate system \, S \, according to the mentioned transformation formulas.
Analogously, the coordinates of a contravariant vector \, \mathbf{v} \, is an \, n-tuple of numbers \, v_k (S), k = 1, 2, \dots, n \, that depends on the coordinate system \, S \, in a different way. (more on this below).
This dependency is characterized by the fact that the “scalar product” \, \sum u_k (S) \, v_k (S) \, of a covariant vector \, \mathbf{u} \, and a contravariant vector \, \mathbf{v} \, is independent of the coordinate system \, S \, and therefore invariant under a change of \, S .
There are also more general, so-called geometric objects (e.g., pseudovectors and tensors) that vary with the coordinate system in other ways.
/////// End of translation from Eriksson, Flerdimensionell analys.
//////////////////////////////////////////////// quoting Wikipedia:
IMPORTANT: The Wikipedia article on the concept of basis for a linear space mistakenly equates the concepts of components and coordinates (probably because there is an isomorphism between them in the most common cases). This mistake is at the root of a fundamental confusion that makes it difficult to understand many important differences, including the difference between covariance and contravariance
Covariance and contravariance of vectors
In physics, especially in multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis. In modern mathematical notation, the role is sometimes swapped. [2]
In physics, a basis is sometimes thought of as a set of reference axes (also known as a frame of reference). A change of scale on the reference axes corresponds to a change of units in the problem. For instance, by changing scale from meters to centimeters (that is, dividing the scale of the reference axes by 100), the coordinates of a measured velocity vector are multiplied by 100.
The coordinates of a vector changes scale inversely to changes in scale of the reference axes, and consequently the vector is called contravariant. As a result, a vector often has units of distance or distance with other units (as, for example, velocity has units of distance divided by time).
In contrast, a covector, also called a dual vector, typically has units of the inverse of distance or the inverse of distance with other units. For example, a gradient has units of a spatial derivative, i.e., distance−1. The coordinates of a covector change in the same way as changes to scale of the reference axes, and consequently a covector is called covariant.
A third concept related to covariance and contravariance is invariance. An example of a physical observable that does not change with a change of scale on the reference axes is the mass of a particle, which has units of mass (that is, no units of distance). The single, scalar value of mass is independent of changes to the scale of the reference axes and consequently is called invariant.
Under more general changes in basis:
A contravariant vector or tangent vector (often abbreviated simply as vector, such as a direction vector or velocity vector) has coordinates that contra-vary with a change of basis to compensate. That is, the matrix that transforms the vector coordinates must be the inverse of the matrix that transforms the basis vectors. Hence the coordinates of contravariant vectors (as opposed to those of covectors) are said to be contravariant. Examples of vectors with contravariant coordinates include the position of an object relative to an observer, or any derivative of position with respect to time, including velocity, acceleration, and jerk.
In Einstein notation (implicit summation over every repeated index), contravariant coordinates are denoted with upper indices as in
\textbf{v} = v^i \textbf{e}_i .
A covariant vector or cotangent vector (often abbreviated as covector) has coordinates that co-vary with a change of basis. That is, the coordinates must be transformed by the same matrix as the change of basis matrix. Examples of covariant vectors generally appear when taking the gradient of a function.
In Einstein notation, covariant coordinates are denoted with lower indices as in
\textbf{w} = w_i \textbf{e}^i .

/////////
A vector, v, represented in terms of tangent basis e1, e2, e3 to the coordinate curves (left),
dual basis, covector basis, or reciprocal basis e1, e2, e3 to coordinate surfaces (right), in 3-d general curvilinear coordinates (q1, q2, q3), a tuple of numbers to define a point in a position space. Note the basis and cobasis (= dual basis = reciprocal basis) coincide only when the basis is orthogonal.[1]
IMPORTANT: Wikipedia is mistaken here. The basis and cobasis (= dual basis = reciprocal basis) coincide only when the basis is orthonormal. In this case the basis is identical to the dual basis
Covariance and contravariance of vectors
Covariant basis and contravariant coordinates give vector invariance
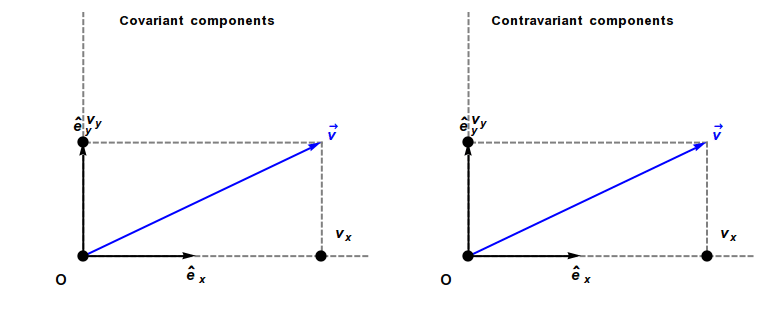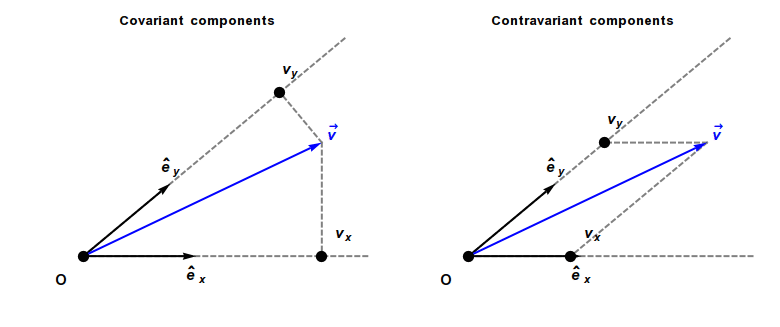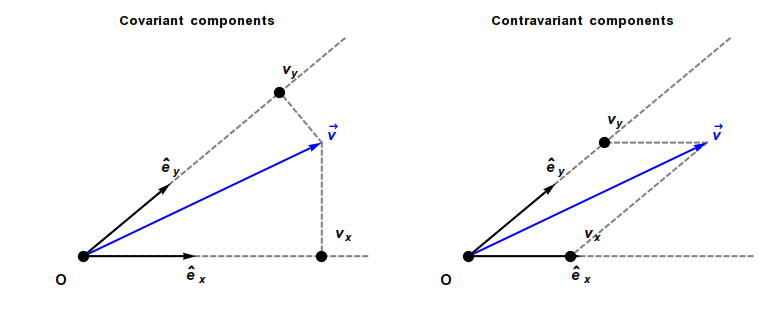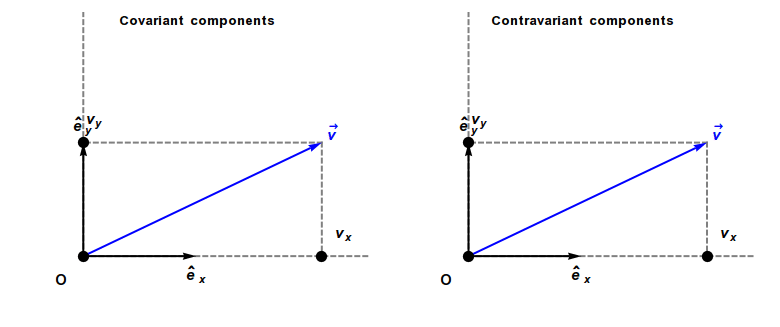
Covariant and contravariant components of a vector

Constructing a covariant basis in one dimension
///////
////////
Dual basis = cobasis = reciprocal basis: (based on Wikipedia)
To perform operations with a vector, we must have a straightforward method of calculating its coordinates (by Wikipedia erroneously equated with its components). In a Cartesian frame, the necessary operation is the dot product of the vector and the corresponding basis vector.
\textbf{x} \equiv x_1 {\textbf{e}}_1 + x_2 {\textbf{e}}_2 + x_3 {\textbf{e}}_3 \equiv (\textbf{x} \cdot \textbf{e}_1) \textbf{e}_1 + (\textbf{x} \cdot \textbf{e}_2) \textbf{e}_2 + (\textbf{x} \cdot \textbf{e}_3) \textbf{e}_3,
where \textbf{e}_k are the basis vectors of the frame. The coordinates of \textbf{x} have been found by:
x_k = \textbf{x} \cdot \textbf{e}_k .
IMPORTANT: Actually the the above is true if and only if the vectors of the Cartesian frame form an orthonormal basis.
In a non-Cartesian frame, we do not necessarily have \textbf{e}_i \cdot \textbf{e}_j = 0 for all i \neq j . However, it is always possible to find a vector \textbf{e}^i such that x^i = \textbf{x} \cdot \textbf{e}^i , (i = 1, 2, 3)
In fact, the equality holds when \textbf{e}^i is the dual basis of \textbf{e}_i (see below). Notice the difference in position of the index i .
In an orthonormal frame we have \textbf{e}^i = \textbf{e}_i .
//////// Explain the concept of dual basis
In linear algebra, given a vector space V with a basis B of vectors indexed by an index set I (the cardinality of I is the dimension of V ), the dual set of B is a set B^* of vectors in the dual space V^* with the same index set I such that B and B^* form a biorthogonal system.
The vectors of the dual set are always linearly independent but they do not necessarily span V^* – unless V is finite dimensional. If they do span V^* , then the vectors of the dual set B^* are called the dual basis or the reciprocal basis of the basis B .
Denoting the indexed vector sets as B = \{ \textbf{e}_i \}_{i \in I} and B^* = \{ \textbf{e}^i \}_{i \in I} , being biorthogonal means that the elements pair to have an inner product equal to 1 if the indexes are equal, and equal to 0 otherwise.
Symbolically, evaluating a dual vector in V^* operating on a vector in the original space V can be expressed as
\textbf{e}^i \cdot \textbf{e}_j = {\delta}^i_j = \begin{cases} 1 &\text{ if } i = j \\0 &\text{ if } i \neq j \end{cases} \; ,
where {\delta}^i_j is the Kronecker delta symbol.
////////