This page is a sub-page of our page on Category Theory.
///////
Related KMR-pages:
• Categorical Informatics
• Functors
• Limits and Colimits
• Functor Categories
• Category of Bundles (over a Base Space)
• Naturally Related Functors and Processes
• Adjoint Functors
• The Human Category
///////
Other relevant sources of information:
• Institutional model theory at Wikipedia
///////
In his overview of the development of institution theory, “Three decades of institution theory”, in Jean-Yves Béziau (ed.), Universal Logic: An Anthology, Springer, pp. 309–322, Razvan Diaconescu (2009), states that
/////// Quote:
30 years have passed since the introduction by Joseph Goguen and Rod Burstall of the concept of ‘institution’ (under the name ‘language’). Since then institution theory has gradually developed from a simple and strikingly elegant general category theoretic formulation of the informal notion of logical system into an important trend of what is now called ‘universal logic’, with substantial applications and implications in both logic and computing science. […]
Institution theory may be the only important trend in universal logic that has emerged from within computing science, the others emerging from logic, and perhaps philosophy. This origin of institution theory may surprise many, since computing science is often blamed for its poor intellectual value. While this perception may be generally correct in average, there are very significant exceptions.
In fact, what is now labelled as ‘computing science’ is hardly a science in the way mathematics or physics are. Some say it is still too young and there was not enough time to coagulate, however one can hear this since 50 years already and probably in the next 50 years too. It may be more realistic to view computing science as a playground were several actors, most notably mathematics, but also logic, engineering, philosophy, sociology, biology, play.
Sometimes an extremely interesting play, which has not only brought significant changes and developments to the actors, but also has revolutionized our scientific thinking in many ways. Institution theory is such an example, the way we think of logic and model theory will never be the same as before.
As the paper included in this anthology shows, the birth of the institution concept came as a response to the population explosion of logical systems in use in specification theory and practice at the time. People felt that many of the theoretical developments (concepts, results, etc.), and even aspects of implementations, are in fact independent of the details of the actual logical systems, that especially in the area of structuring of specifications or programs, it would be possible to develop the things in a completely generic way. The benefit would be not only in uniformity, but also in clarity since for many aspects of specification theory the concrete details of actual logical systems may appear as irrelevant, with the only role being to suffocate the understanding. The first step to achieve this was to come up with a very general formal definition for the informal concept of logical system.
Due to their generality, category-theoretic concepts appeared as ideal tools. However there is something else which makes category theory so important for this aim: its deeply embedded non-substantialist thinking which gives prominence to the relationships (morphisms) between objects in the detriment of their internal structure.
Moreover, category theory was at that time, and continues even now to be so, the mathematical field of the utmost importance for computing science. In fact, it was computing science which recovered the status of category theory, at the time much diminished in conventional mathematical areas. The essay that Joseph Goguen wrote remains one of the most beautiful essays on the significance of category theory for computing science – and not only for computing science.
//////// End of Quote
1. Theory of Institutions
////// based on (Goguen & Burnstall, 1992)
Quoting Goguen & Burstall (1992, p. 1):
Abstract
There is a population explosion among logical systems used in Computing Science. Examples include first order logic, equational logic, Horn clause logic, higher order logic, infinitary logic, dynamic logic, intuitionistic logic, order-sorted logic, and temporal logic; moreover, there is a tendency for each theorem prover to have its own idiosyncractic logical system.
We introduce the concept of institution to formalize the informal notion of “logical system.” The major requirement is that there is a satisfaction relation between models and sentences which is consistent under change of notation. Institutions enable us to abstract from syntactic and semantic detail when working on language structure “in the large”; for example, we can define language features for building large structures from smaller ones, possibly involving parameters, without commitment to any particular logical system. This applies to both specification languages and programming languages. Institutions also have applications to such areas as database theory and the semantics of artificial and natural languages.
A first main result of this paper says that any institution such that signatures (which define notation) can be glued together, also allows gluing together theories (which are just collections of sentences over a fixed signature). A second main result considers when theory structuring is preserved by institution morphisms. A third main result gives conditions under which it is sound to use a theorem prover for one institution on theories from another. A fourth main result shows how to extend institutions so that their theories may include, in addition to the original sentences, various kinds of constraints that are useful for defining abstract data types, including both “data” and “hierarchy” constraints. Further results show how to define institutions that allow sentences and constraints from two or more institutions. All our general results apply to such “duplex” or “multiplex” institutions.
/////// End of quote from Goguen & Burstall
Quoting Goguen & Burstall (1992, p. 2):
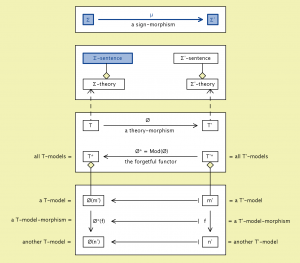
One of the most essential elements of a logical system is its relationship of satisfaction between its syntax (i.e., its sentences) and its semantics (i.e., its models); this relationship is sometimes called a “model theory” and classically appear[s] in the form of a Galois connection (as in section 2.2 below). Whereas traditional model theory assumes a fixed vocabulary, institutions allow us to consider many different vocabularies at once. Informally, an institution consists of
• a collection of signatures (which are vocabularies for use in constructing sentences in a logical system) and signature morphisms, together with for each signature ∑,
• a collection of ∑-sentences,
• a collection of ∑-models, and
• a ∑-satisfaction relation, of ∑-sentences by ∑-models,
such that when you change signatures (by a signature morphism), satisfaction of sentences by models changes consistently.
/////// End of quote from Goguen & Burstall
Quoting Goguen & Burstall (1992, p. 4):
Systematic program design requires a careful specification of the problem to be solved. But experience in software engineering shows that there are major difficulties in producing consistent, rigorous specifications that adequately reflect users’ requirements for complex systems. We suggest that these difficulties can be ameliorated by making specifications as modular as possible, so that they are built from small, understandable pieces, many of which may be used repeatedly (for example, those defining concepts like “ordering”, “list”, or “file”).
Modern work in programming methodology supports the view that abstraction, and in particular data abstraction, is a useful way to obtain such modularity, and that parameterized (also called “generic”) specifications can lead to further improvements.
One way to apply these ideas is through a specification language that supports putting together parameterised abstractions. Whereas a specification written directly in a logical system is an unstructured, and possibly unmanageably large, collection of sentences, a specification language can make it much easier to write and read specifications, especially for large systems. […]
We also suggest that modularity may be useful in proving theorems about specifications, for example, in proving that a given program actually meets its specification. Moreover, exactly the same structuring mechanisms can be used to achieve exactly the same advantages in programming languages that are rigorously based upon some formal system of logic; we shall call such languages logical programming languages. Finally, the same techniques of modularisation can be applied to conventional imperative programming languages such as Ada, by using a system like LIL [39, 104].
In order for a specification written in a given language to have precise meaning, it is necessary for that language to have a precise semantics. (This may seem obvious, but the fact is that many specification languages lack such a semantics). Part of that semantics will be an underlying logical system, which must have certain properties to be useful for this task.
These include suitable notions of model and sentence, and a satisfaction relationship between sentences and models that is invariant under change of notation. For applications to programming we will want to define models by programs.
Signature morphisms play a basic role in structuring specifications. Let us assume for concreteness of exposition that the signatures have sorts and operators, and then consider some specific structuring mechanisms.
First, we may build a more complex specification by adding new sorts and operators to an existing signature; then the inclusion of the original signature into the extended signature is an “enrichment” signature morphism.
Second, we may wish to use such an enrichment not just as one specification, but on a whole class of specifications. This leads to parametrised specifications. For instantiation, the parameter ‘sorts’ and ‘operators’ are bound to particular sorts and operators by a “binding” signature morphism.
Third, a large specification may have name clashes: two sub-specifications may happen to use the same sort or operator names. These can be eliminated by signature morphisms that define renamings.
Enrichment, binding and renaming raise no deep logical problems, but are still important for modular structure. Using institutions, we can define such features without making a commitment to any particular logical systems. Moreover, the task of giving a semantics for the language is also simplified. We feel that these considerations justify an attempt to deal with logical systems in a general way, free of the entanglements of any particular syntax and semantics.
/////// End of quote from Goguen & Burstall
Quoting Goguen & Burstall (1992, p. 9):
An institution consists of a category of signatures such that associated with each signature are sentences, models, and a relationship of satisfaction that, in a certain sense, is invariant under change of signature. Two familiar examples of this setup are equational logic (also called general, or universal, algebra) and first order logic (or model theory).
In equational logic, a signature declares the function symbols that are available, -sentences are equations using these function symbols, and -models are -algebras. In first order logic, signatures in addition give relation symbols, sentences are the usual first order sentences, and models are the usual first order structures. In both cases, satisfaction is the familiar relation. […]
The essence of the institution notion is that a change of signature (by a signature morphism) induces “consistent” changes in sentences and models, in a sense made precise by the “Satisfaction Condition” in Definition 1 below.
This goes a step beyond Tarski’s classic “semantic definition of truth” [102], and also generalizes Barwise’s “Translation Axiom” [6]. The wide range of consequences, and the fact that even for equational logic, the Satisfaction Condition is not entirely trivial, suggest that this step has some substance. Moreover, it is a basic and familiar fact that the truth of a sentence (in logic) is independent of the symbols chosen to represent its functions and relations. This can be summed up in the slogan
Truth is invariant under change of notation.
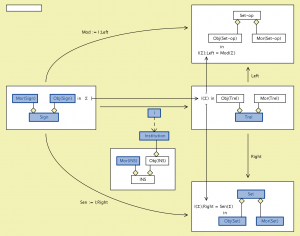
It is also fundamental that sentences translate in the same direction as the change of notation, whereas models translate in the opposite direction. Because reversing the direction of morphisms gives a contravariant functor, the definition below uses , the opposite of the category of categories.
///////
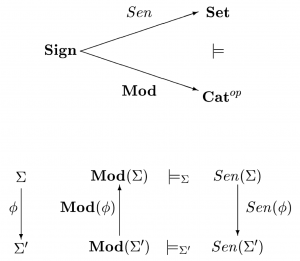
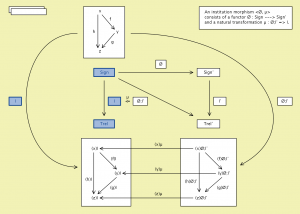
Definition 1: An institution \, \mathscr{I} \, consists of
1) a category Sign whose objects are called signatures,
2) a functor Sen : Sign \, \rightarrow \, Set , giving for each signature a set whose elements are called sentences over that signature,
3) A functor Mod : Sign \, \rightarrow \, Cat^op giving for each signature ∑ a category whose objects are called ∑-models, and whose arrows are called ∑-(model) morphisms, and
4) a relation \, {\models}_{\Sigma} \subseteq | Mod(\Sigma)| \, \times Sen(\Sigma) \, for each \, \Sigma \in | Sign | \,
called ∑-satisfaction, such that for each morphism \, \phi \, : \Sigma \rightarrow \Sigma' \, in Sign,
the Satisfaction Condition
\, m' \, {\models}_{\Sigma'} \, Sen(\phi)(e) \, if and only if \, Mod(\phi)(m') \, {\models}_{\Sigma} \; e \,
holds for each \, m' \in | Mod(\Sigma') | \, and each \, e \in Sen(\Sigma) .
We will write \, \phi(e) \, or even \, \phi e \, for \, Sen(\phi)(e) \, , and \, \phi(m')\, or \, \phi m' \, for Mod(\phi)(m') \, ; also we will drop the signature subscripts on the satisfaction relation
when it is not confusing.
These conventions are used in the following condensed form of the Satisfaction Condition:
\, m' \, \models \, \phi e \, if and only if \, \phi m' \, \models \, e .
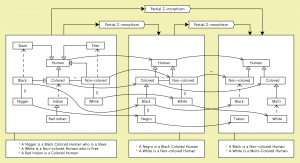
The following picture may help in visualizing these relationships:
Appendix A of this paper shows that a number of logical systems satisfy Definition 1, including (the many-sorted versions of) equational logic, first order logic, Horn clause logic, Horn clause logic with equality, and first order logic with equality. We note that it can be non-trivial to establish the Satisfaction Condition.
For some purposes, Definition 1 can be simplified by replacing Mod : Sign \, \rightarrow \, Cat^op by a functor Mod : Sign \, \rightarrow \, Set^op, where Mod(\Sigma) = \, | Mod(\Sigma)| \, is the collection of all ∑-models; the two versions are thus related by the equation ???????. Indeed, this was our original version [17].
Some reasons for changing it are: first, it is more consistent with the categorical point of view to consider morphisms of models along with models; and second, we want every liberal institution to be an institution, rather than just to determine one (liberal institutions are discussed later in this paper).
Section 2.5 gives a more categorical definition of institutions which replaces the perhaps ad hoc looking family of satisfaction relations by a functor into a category of “twisted relations.” This more categorical formulation suggests some further generalisations of the institution concept, including one which models deductions as morphisms among sentences.
/////// End of quote from Goguen & Burstall
/////// Conzilla maps:
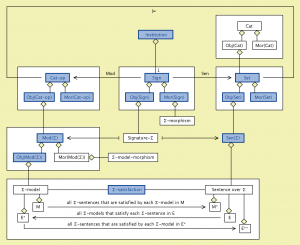
Institution:
///////
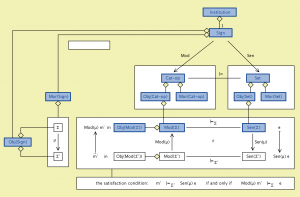
Institution-satisfaction:
///////
The category of twisted relations (Trel):
///////
Institution – more categorical definition:
///////
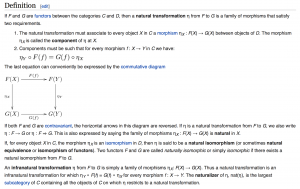
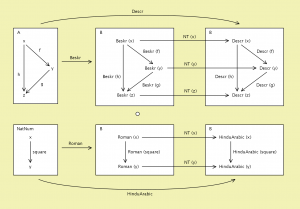
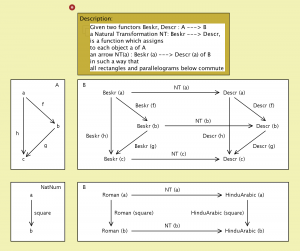
Natural transformation:
///////
Natural transformation of Beskrivning –> Description:
///////
Beskr—>Descr (Nat-Transf):
///////
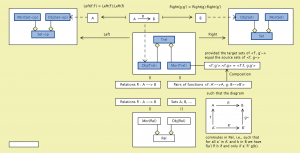
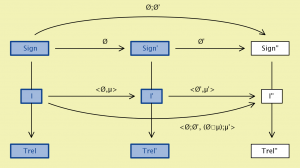
Institution Morphism:
///////
Composition of Institution Morphisms:
///////
Theory morphisms forgetful functor:
///////
Provider/Aggregator Institutions:
///////
An example of partial ∑-morphisms:
///////