This page is a sub-page of our page on Category Theory.
///////
Pullback of a Functor Category:
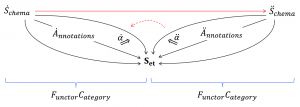
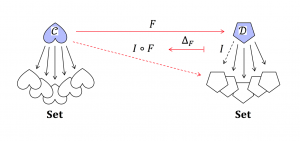
A Schema Mapping \, F \, and its corresponding Pullback Functor \, { \triangle }_F \,:
Translating from annotation-i to annotation-k:
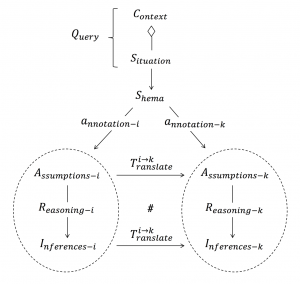
Notation: If the above diagram commutes (as is indicated by the # sign), the annotation-k is said to be naturally related to the annotation-i. Natural relationships are indicated by “implication arrows”, as seen in the diagram below.
Process B is naturally related to process A:
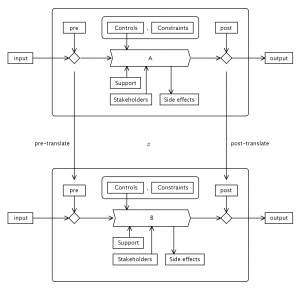
///////
Numbers are naturally related to Music:
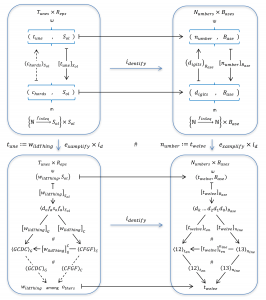
Numbers and Vectors are naturally equivalent:

Numbers and Vectors are naturally related to Music:
